Introdução
A ligação entre inteligência, desenvolvimento econômico e produção científica desperta certo interesse. Desde a Revolução Científica, quando Galileu e Newton desafiaram os paradigmas do conhecimento, até os dias atuais, com os avanços em inteligência artificial, o saber esteve no centro das grandes transformações da humanidade. Mas o que realmente impulsiona esse avanço?
Entre os símbolos máximos da inovação e do avanço científico está o Prêmio Nobel, uma honraria concedida às mentes que mais contribuíram para o progresso do conhecimento. Algumas nações acumulam dezenas, até centenas de premiações, enquanto outras mal figuram nas estatísticas. Essa disparidade levanta uma reflexão:
Será que países com mais laureados possuem QI médio mais alto ou o Prêmio Nobel reflete sobretudo o investimento em ciência e educação?
Para entender melhor essas relações, recorremos a uma ferramenta fundamental da estatística: o coeficiente de correlação. A análise parte da base de dados Average global IQ per country with other stats1 (disponível no Kaggle) extraída do Programa das Nações Unidas para o Desenvolvimento (também conhecido internacionalmente como United Nations Development Programme), que inclui informações sobre Índice de Desenvolvimento Humano (IDH), escolaridade e renda nacional bruta dos países. A base também conta com informações sobre QI médio e o número de Prêmios Nobel.
Pacotes a serem utilizados
library(tidyverse)
library(janitor)
library(ggcorrplot)
Caso estes pacotes não estejam instalados, executar comando abaixo.
install.packages("tidyverse")
install.packages("janitor")
install.packages("ggcorrplot")
Importação de dados
Para esta análise utilizamos o arquivo avgIQpercountry.csv2 que reúne informações sobre o QI médio por país. Além dele, há também o iq_classification.csv, que classifica os níveis de QI em “Gênio”, “Dotado”, “Acima da média”, e entre outras categorias, de acordo com a faixa de pontuação. Todavia, esse segundo arquivo não será abordado neste artigo.
Afim de facilitar a replicação da análise apresentada neste artigo, disponibilizei os dados no meu GitHub. Se preferir, você também pode baixá-los diretamente do Kaggle – basta conferir a nota de rodapé e a seção Referências ao final.
url <- "https://raw.githubusercontent.com/drewmelo/blogr/master/content/post/2025-03-09-qi-vs-desenvolvimento-o-dinheiro-compra-intelig-ncia/dados/avgIQpercountry.csv"
A partir disso, podemos importar os nossos dados:
df <- read_csv(url) |>
drop_na() |>
clean_names() |>
select(!c(continent, literacy_rate)) |>
mutate(population_2023 = as.numeric(population_2023))
# Visualizando estrutura dos dados
glimpse(df)
## Rows: 179
## Columns: 8
## $ rank <dbl> 1, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 1…
## $ country <chr> "Japan", "Singapore", "Hong Kong", "China…
## $ average_iq <dbl> 106.48, 105.89, 105.37, 104.10, 102.35, 1…
## $ nobel_prices <dbl> 29, 0, 1, 8, 0, 2, 5, 0, 111, 22, 0, 2, 0…
## $ hdi_2021 <dbl> 0.925, 0.939, 0.952, 0.768, 0.925, 0.808,…
## $ mean_years_of_schooling_2021 <dbl> 13.4, 11.9, 12.2, 7.6, 12.5, 12.1, 12.9, …
## $ gni_2021 <dbl> 42274, 90919, 62607, 17504, 44501, 18849,…
## $ population_2023 <dbl> 1.232945e+08, 6.014723e+06, 7.491609e+06,…
Removemos os valores ausentes (NA) que aparecem nas variáveis hdi_2021, mean_years_of_schooling_2021 e
gni_2021. Se não fossem eliminados, a correlação retornaria um resultado inválido (NA), a menos que o argumento
use = "pairwise.complete.obs" fosse especificado na função cor().
O papel do IDH na inteligência média dos países
Para começar nossa análise podemos pegar e quantificar a relação entre as variaveis average_iq e
hdi_2021. A correlação é feita através da função cor()
cor(df$average_iq, df$hdi_2021)
## [1] 0.7554595
Por meio do resultado pode-se observar uma correlação positiva forte entre essas variáveis. Mas como posso afirmar que é uma correlação positiva forte? Vejamos
-
Se $ r $ for positivo (isto é, $ r $ > 0), há uma relação direta: conforme uma variável aumenta, a outra tende a crescer também.
-
Se $ r $ for negativo (isto é, $ r $ < 0), a relação é inversa: o aumento de uma variável está associado à redução da outra.
-
Se $ r = 0$, não há correlação, e se o valor estiver muito próximo de zero, a relação pode ser considerada inexistente.
Correlações perfeitas ocorrem quando $ r $ é exatamente 1 (positiva) ou -1 (negativa), mas esse cenário tende a ser raro na maioria das análises.
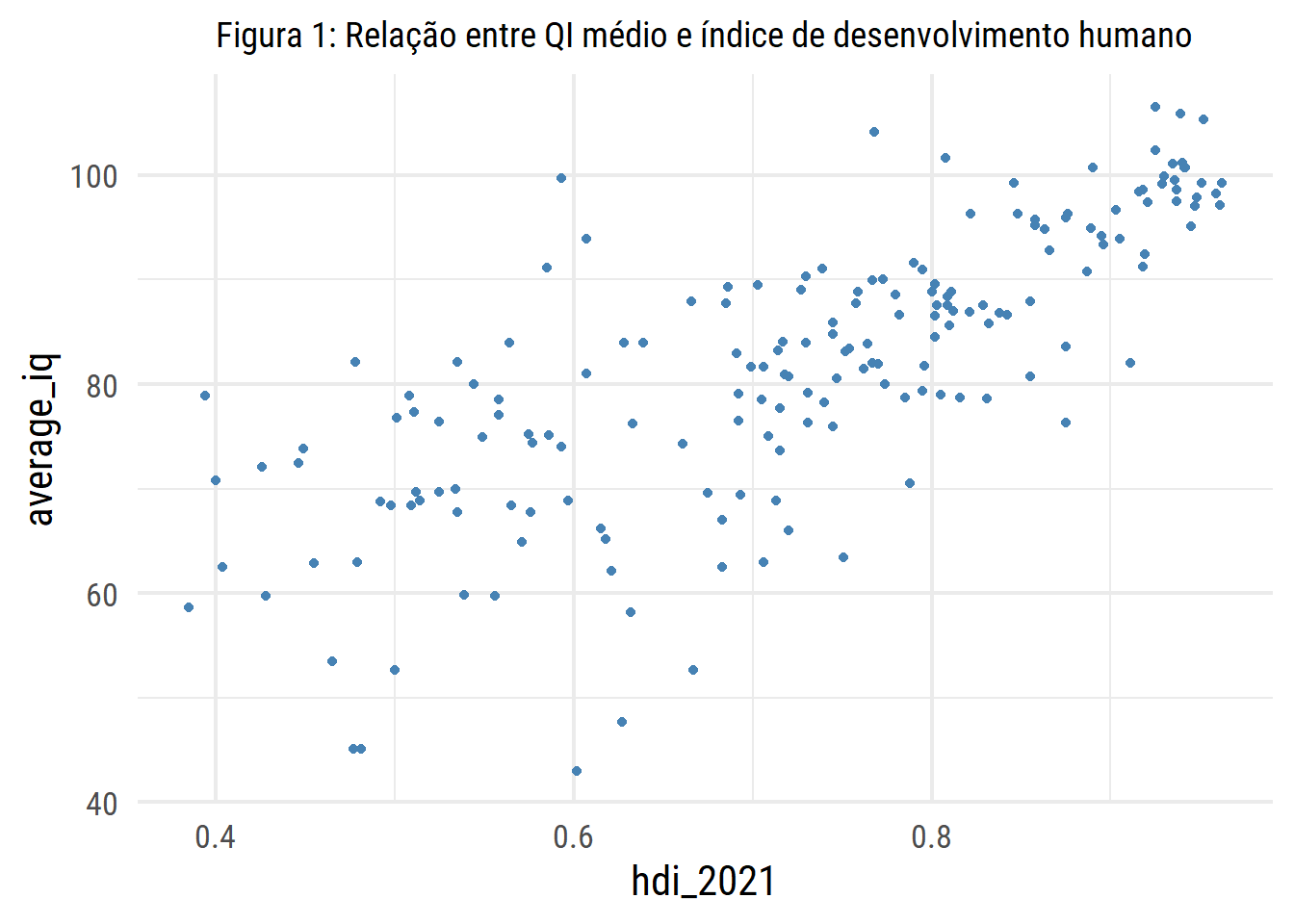
No caso em questão, o IDH apresenta uma correlação de 0,755 com o QI médio dos países. Mas como interpretar este resultado? Bem, podemos dizer que quanto maior o nível de desenvolvimento humano, maior tende a ser o QI médio. Vale lembrar que correlação não implica causalidade, mesmo que os dados mostrem que melhores condições de vida e acesso à educação podem favorecer o desenvolvimento cognitivo de uma população.
A visualização dos dados ficaria dessa forma:
df |>
ggplot(aes(x = hdi_2021, y = average_iq)) +
geom_point(col = 'steelblue') +
theme_minimal()
Tipos de correlação em estatística
Por padrão, a função cor() calcula o coeficiente de correlação de Pearson, cuja fórmula é dada por:
$$
r = \frac{ \sum_{i = 1}^{n} \left( x_{i}- \overline{x} \right) \left( y_{i}- \overline{y} \right)}{ \sqrt{ \left[ \sum_{i = 1}^{n} \left( x_{i}- \overline{x} \right)^{2} \right] \left[ \sum_{i = 1}^{n} \left( y_{i}- \overline{y} \right)^{2} \right]}} \tag{1}
$$
onde
-
$ x_i, \ y_i $ são os valores individuais das variáveis $ X $ e $ Y $
-
$ \bar{x}, \bar{y} $ são as médias de $ X $ e $ Y $
Na Equação 1 o numerador pode ser representado como $ Cov(X, \ Y) $, que corresponde à covariância, ou seja, à média dos produtos dos valores centrados das variáveis. Já o denominador contém $ S_x $ e $ S_y $, que representam os desvios padrões amostrais de cada variável (ver Equação 2).
$$ r = \frac{Cov(X, Y)}{S_x \times S_y} \tag{2} $$
No nosso caso, $ X $ corresponde à variável hdi_2021 e $ Y $ a average_iq, o qual é facilmente visto na Figura 1. O mesmo pode ser feito com outras variáveis, que é o que faremos neste artigo.
Além da correlação de pearson, a função cor() permite outros métodos de cálculo:
-
cor(x, y, method = "spearman")mede a correlação com base no rank (posição) dos valores, em vez dos valores absolutos. Por ser uma medida não paramétrica, é útil quando os dados não seguem uma distribuição normal. -
cor(x, y, method = "kendall")avalia a concordância entre as ordens dos valores das variáveis, ou seja, verifica se a relação entre elas se mantém ordenada (exemplo: pares concordantes e discordantes). Além de ser menos sensível a outliers.
Educação e riqueza: qual influencia mais no QI médio?
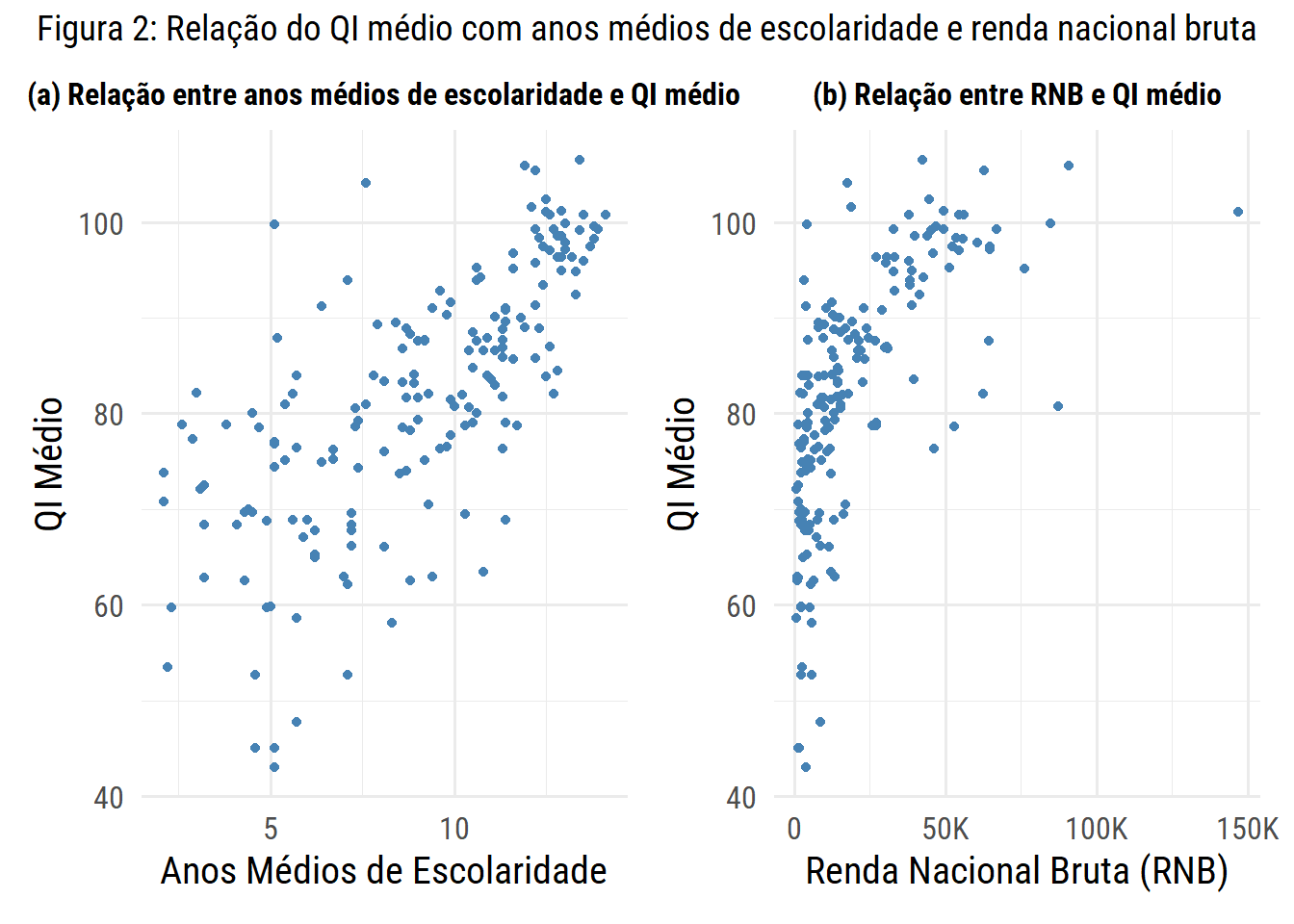
Ao analisarmos outras variáveis também podemos observar a relação entre o QI médio e a média de anos de escolaridade.
cor(df$average_iq, df$mean_years_of_schooling_2021)
## [1] 0.7054428
Ou alternativamente:
cor(df$average_iq, df$gni_2021)
## [1] 0.6348542
Os resultados mostram uma forte correlação positiva entre o QI médio e a renda nacional bruta, ou neste caso, países mais ricos tendem a apresentar populações com elevada inteligência média. Entretanto, mesmo que a relação com a renda nacional bruta seja moderadamente forte (0,635), ela não chega a ser tão robusta quanto a observada com o IDH (0,755) e os anos médios de escolaridade (0,705).
Mas o que isso quer dizer, afinal?
Através dessas comparações e como os dados mostram, fatores como educação e qualidade de vida apresentam correlação mais forte com o desenvolvimento cognitivo da população do que a renda nacional bruta isoladamente. A renda pode ser um reflexo de melhores condições gerais, mas é o acesso ao conhecimento e às oportunidades que parecem desempenhar um papel mais decisivo.
Gigantes invisíveis ou viés histórico?
A relação entre o tamanho da população de um país e o número de Prêmios Nobel concedidos a seus cidadãos parece óbvia. Quanto mais habitantes, maior a chance de surgir um gênio, certo? Mas os dados contam outra história.
Se olharmos apenas para os números absolutos, os Estados Unidos aparecem como líderes em Prêmios Nobel, enquanto China e Índia se tornam praticamente invisíveis. Esse tipo de comparação, porém, desconsidera um aspecto fundamental: o tamanho da população. Para tornar a análise mais justa, faz sentido calcular o número de prêmios por milhão de habitantes.
Os Estados Unidos acumulam 400 Prêmios Nobel para uma população de 340 milhões de pessoas, o que equivale a 1,18 prêmios por milhão de habitantes. Já o Reino Unido, com 137 prêmios e apenas 67,7 milhões de habitantes, registra uma taxa de 2,02 prêmios por milhão, sendo a mais alta entre os países analisados. A China, apesar de ter 1,4 bilhão de habitantes e possuir apenas 8 Prêmios Nobel, possui uma taxa de 0,006 prêmios por milhão.
Esses números mostram que uma população numerosa não garante uma produção científica de forma proporcional. Países menores, mas com tradição científica já estabelecida, como Reino Unido e Alemanha, acabam exercendo um papel desproporcionalmente grande na produção intelectual global. Vemos que o avanço do conhecimento não depende apenas da quantidade de habitantes, mas da prioridade que cada nação dá à ciência.
Para entender melhor a relação entre os dados que mencionamos anteriormente podemos ver que a correlação entre população e Prêmios Nobel foi de 0,16, praticamente inexistente, neste caso.
cor(df$population_2023, df$nobel_prices)
## [1] 0.1641867
Quando os números contam histórias diferentes
Existem vários métodos estatísticos para detectar pontos extremos em relação a distribuição dos dados, um exemplo é a distância interquatil. De forma bem resumida, esse ponto extremo (ou outlier, como é encontrado na literatura) seria um valor muito distante da média geral, podendo representar tanto especificidades interessantes quanto possíveis erros. Contudo, como nosso objetivo aqui é apresentar a relação geral entre as variáveis, deixaremos essa investigação mais detalhada dos outliers para um futuro artigo.
# Para a variável população
outliers_varx <- boxplot.stats(df$population_2023)$out
# Para a variável prêmio nobel
outliers_vary <- boxplot.stats(df$nobel_prices)$out
Aplicamos, então, um filtro para retirar esses valores da base de dados.
df_outlier <- df |>
filter(!population_2023 %in% outliers_varx & nobel_prices %in% outliers_vary)
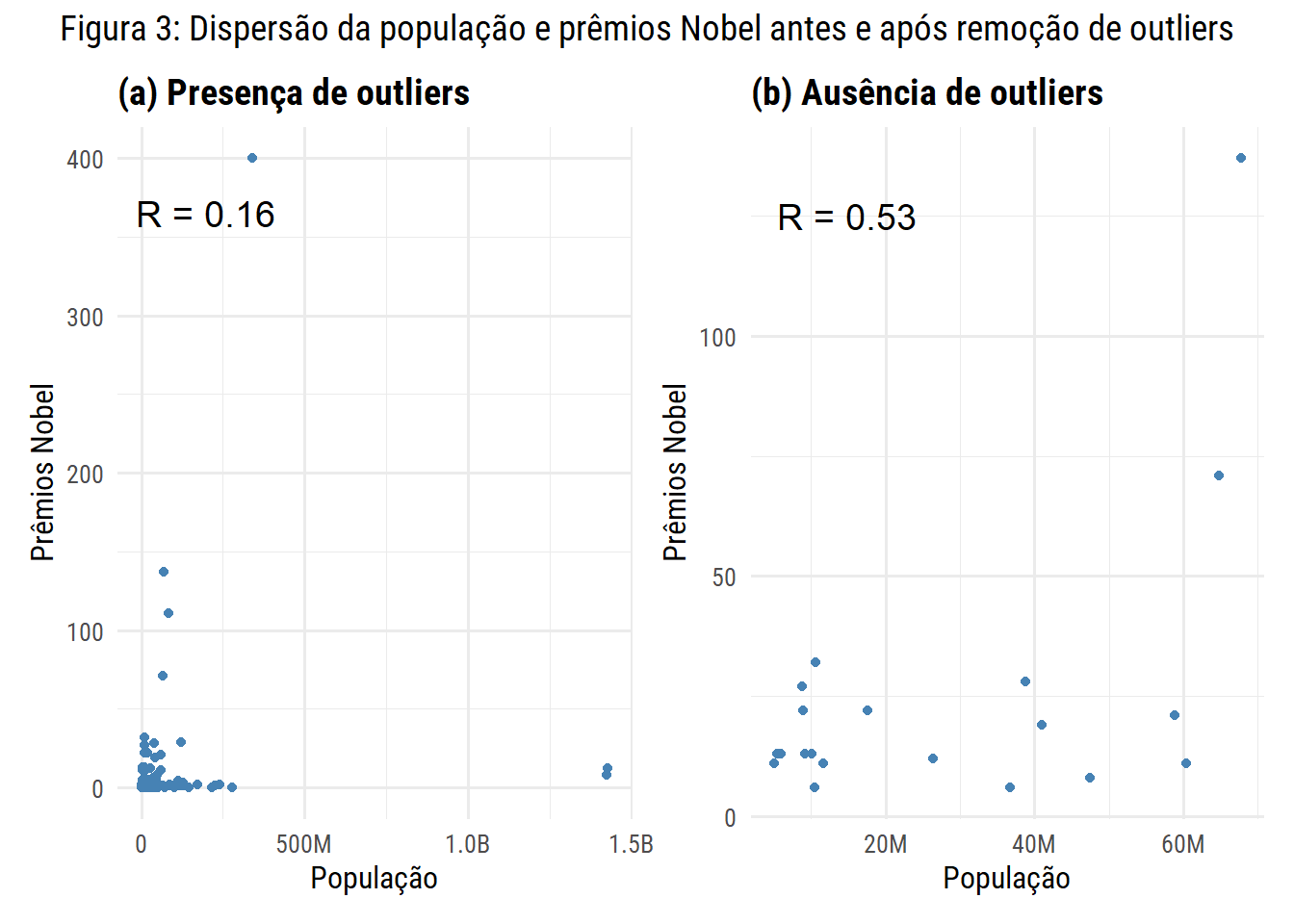
Deixamos a cargo do leitor para plotar o objeto df_outlier em um gráfico de dispersão (representado na Figura 3(a)), semelhante ao que fizemos na Seção 2. O papel do IDH na inteligência média dos países.
A remoção dos outliers alterou substancialmente o resultado, elevando a correlação para 0,53, como ilustrado na Figura (b). Uma relação torna-se exposta e contrária ao que presenciamos anteriormente: entre países de porte médio, aqueles com maior população passaram a exibir uma tendência de acumular Prêmios Nobel. Porém esse ajuste traz um dilema, ao excluir outliers deixamos de fora as grandes potências científicas, como os Estados Unidos, que dominam o Prêmio Nobel.
Tal ocorrência nos levanta uma importante questão:
Até que ponto remover valores extremos ajuda a compreender melhor um fenômeno sem perder parte do contexto da nossa análise?
No fim das contas, esse é um exemplo perfeito de como a estatística pode nos fazer ver padrões diferentes dependendo de como tratamos os dados. Como Darrell Huff argumenta em Como Mentir com Estatística, os números, por si só, não contam toda a verdade — é a forma como os apresentamos que molda a narrativa.
Além da correlação de Pearson
Para evitar o tipo de situação anterior é importante destacar que, em um estudo de alcance global, a remoção de outliers nem sempre seria justificável. Além do risco de eliminar informações relevantes, reduzir demais a amostra pode comprometer a representatividade dos dados.
Como mencionado na Seção 2.1. Tipos de correlação em estatística, há diferentes formas de calcular o coeficiente de correlação. O método de Pearson, por sua vez, resultou em uma correlação de 0,16 entre população e Prêmios Nobel. Quando aplicamos o método de Kendall, que é mais resistente para dados com outliers ou relações não lineares, o coeficiente aumentou para 0,29. Ainda é uma correlação fraca, mas um pouco mais crível.
cor(df$population_2023, df$nobel_prices, method = "kendall")
## [1] 0.2895059
Se a análise envolver variáveis ordinais, como rankings, o coeficiente de Spearman pode ser mais adequado.
cor(df$rank, df$hdi_2021, method = "spearman")
## [1] -0.7945742
A variável rank representa a posição dos países em um determinado ranking, como primeiro, segundo, terceiro lugar e assim por diante. Quando esse ranking se refere ao QI médio, é natural observar que países mais bem posicionados (com valores menores de rank) tendem a apresentar um IDH mais elevado. A relação inversa entre essas duas variáveis explica a forte correlação negativa.
Matriz de correlações
Outra abordagem, bastante útil por sinal, é a matriz de correlações, que nos ajuda a visualizar de forma geral
as relações entre todas as variáveis em vez de calcular coeficientes separadamente. Assim como ocorre com o resultado da função cor(), cada célula dessa matriz contém um valor entre -1 e 1 entre uma variável (linha) e outra variável (coluna).
matriz_corr <- df |>
select(!country) |>
cor()
matriz_corr
## rank average_iq nobel_prices hdi_2021
## rank 1.00000000 -0.97445416 -0.2302831 -0.77737636
## average_iq -0.97445416 1.00000000 0.2144355 0.75545950
## nobel_prices -0.23028314 0.21443550 1.0000000 0.23089587
## hdi_2021 -0.77737636 0.75545950 0.2308959 1.00000000
## mean_years_of_schooling_2021 -0.72746085 0.70544282 0.2339327 0.91475026
## gni_2021 -0.66128515 0.63485419 0.2692844 0.78779905
## population_2023 -0.04848491 0.07333404 0.1641867 -0.02836039
## mean_years_of_schooling_2021 gni_2021
## rank -0.72746085 -0.66128515
## average_iq 0.70544282 0.63485419
## nobel_prices 0.23393267 0.26928442
## hdi_2021 0.91475026 0.78779905
## mean_years_of_schooling_2021 1.00000000 0.66183364
## gni_2021 0.66183364 1.00000000
## population_2023 -0.07112675 -0.05311802
## population_2023
## rank -0.04848491
## average_iq 0.07333404
## nobel_prices 0.16418671
## hdi_2021 -0.02836039
## mean_years_of_schooling_2021 -0.07112675
## gni_2021 -0.05311802
## population_2023 1.00000000
E graficamente, teriamos esta representação:
ggcorrplot(matriz_corr, lab = T)
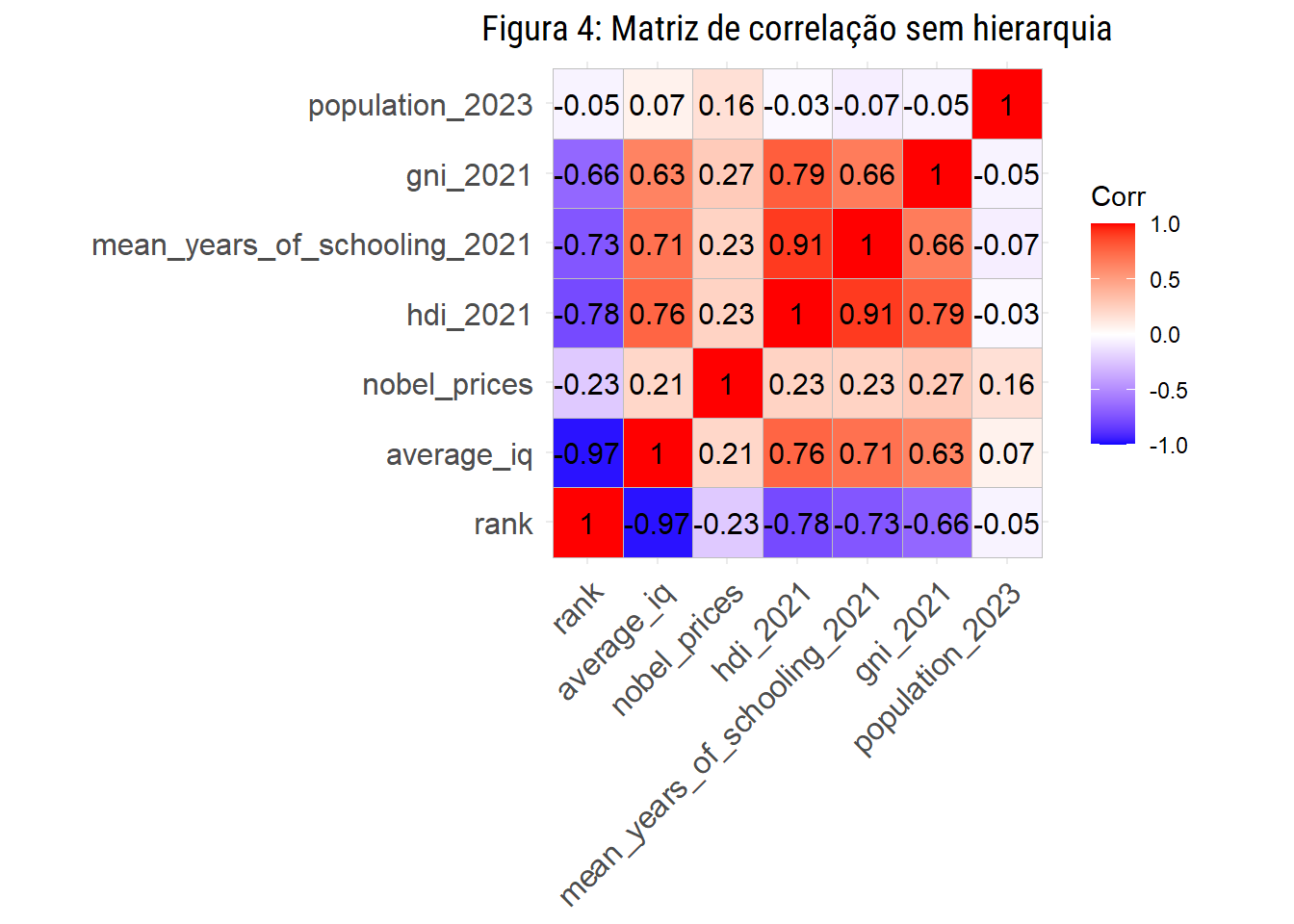
Se quisermos melhorar a apresentação podemos ordenar os coeficientes de correlação hierarquicamente e exibir apenas a metade inferior da matriz, de forma a eliminar redundâncias e tornar a leitura mais intuitiva.
ggcorrplot(matriz_corr, lab = T,
hc.order = T, type = "lower",
outline.color = "white")
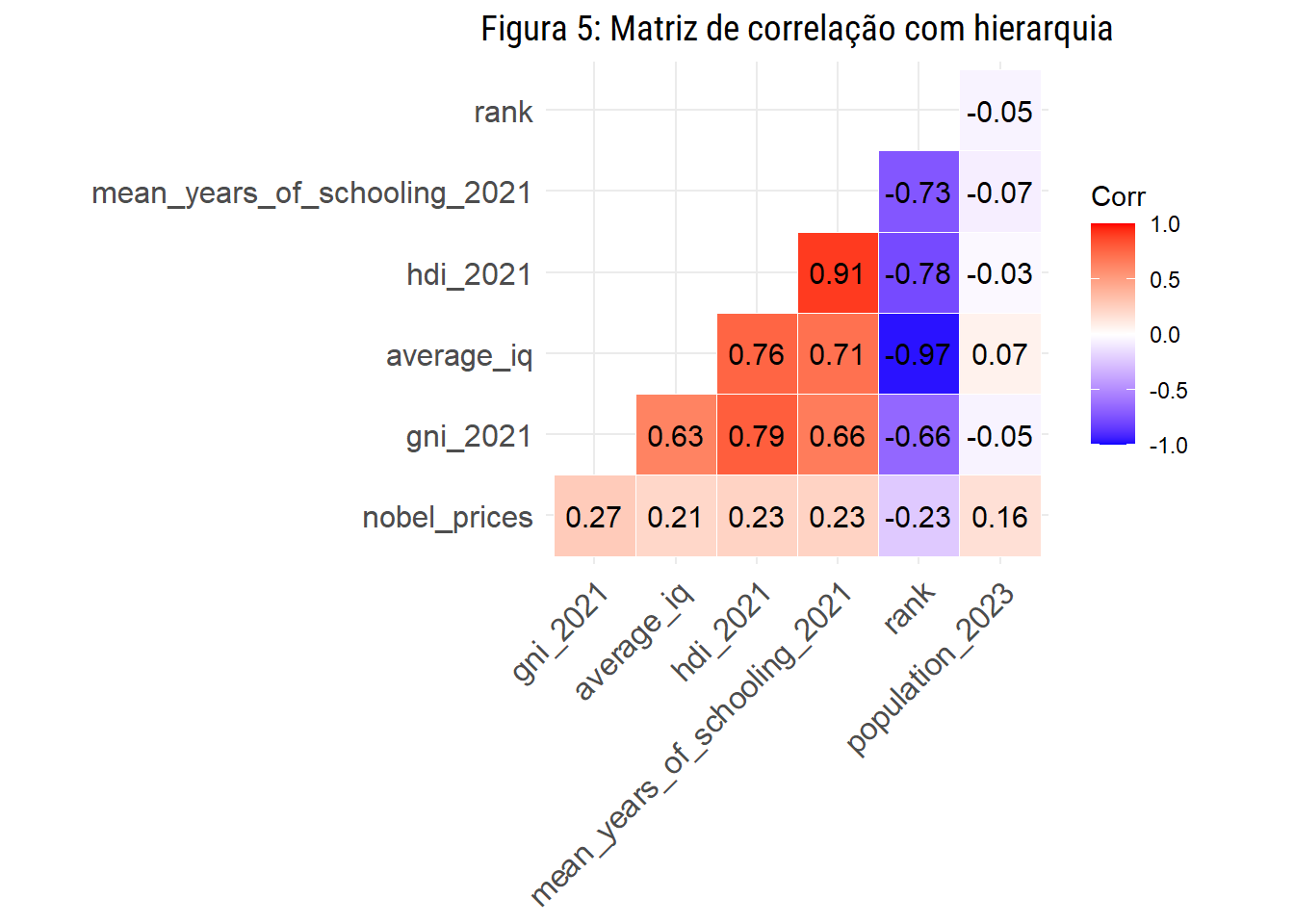
E então, dinheiro compra inteligência?
Ao longo desta análise investigamos a relação entre o QI médio e diferentes indicadores de desenvolvimento econômico, como o IDH, a média de escolaridade, a renda nacional bruta, além do número de Prêmios Nobel conquistados. A questão central — se o dinheiro pode comprar inteligência — não tem uma resposta simples.
Os dados sugerem que países com IDH elevado e maior acesso à educação costumam apresentar um QI médio mais alto. A forte correlação entre essas variáveis mostra que um ambiente propício ao aprendizado e à qualidade de vida influencia diretamente o desenvolvimento cognitivo da população. Já a relação com a riqueza isolada, medida pela renda nacional bruta, é menos evidente. Uma economia forte, por si só, não garante uma população mais inteligente, a menos que os recursos sejam direcionados para educação e bem-estar social.
A distribuição dos prêmios Nobel nos reforça essa complexidade. Países populosos, como China e Índia, não necessariamente acumulam mais laureados, enquanto nações menores, como Reino Unido e Alemanha, concentram grande parte das premiações.
Vale ressaltar que, embora os dados mostrem padrões interessantes, isso não significa que uma variável seja a causa direta da outra. O fato de países com maior IDH e mais anos de escolaridade apresentarem QI médio mais alto não implica, necessariamente, que um fator seja a causa direta do outro. Assim como inteligência e inovação não surgem apenas da riqueza ou do tamanho da população, mas de um ambiente que amplie o acesso ao conhecimento e estimule a pesquisa. Se há algo que os dados deixam claro, como também me arrisco a afirmar, é que o progresso intelectual de um país não está no dinheiro em si, mas na forma como ele é investido.
Eaí, o que você acha? Concorda, discorda ou tem algo a acrescentar? Comente abaixo e reaja ao post!
Referências
BUSSAB, Wilton de Oliveira; MORETTIN, Pedro Alberto. Estatística Básica. 10. ed. São Paulo: Saraiva Uni, 2023. 624 p. ISBN 978-6587958491.
MLIPPO. Average global IQ per country with other stats. Kaggle, 2024. Disponível em: https://www.kaggle.com/datasets/mlippo/average-global-iq-per-country-with-other-stats . Acesso em: 12 mar. 2025.
HUFF, Darrell. Como mentir com estatística. Editora Intrinseca, 2016.
