
Introdução
A teoria dos jogos é um ramo da matemática que explora as interações estratégicas em que as decisões de um indivíduo são influenciadas pelo conflito e cooperação de outros participantes. Em relação ao campo das ciências econômicas, essa teoria desempenha um papel fundamental ao analisar como as pessoas realizam escolhas estratégicas diante de objetivos concorrentes em um contexto de escassez.
Uma aplicação interessante da teoria dos jogos na área da economia é a sua combinação com simulações de aprendizado. Por exemplo, em um cenário em que diferentes empresas competem para estabelecer preços em um mercado, é possível utilizar a teoria dos jogos em conjunto com modelos de aprendizado. Nesses modelos, as empresas podem aprender ao longo do tempo a tomar decisões estratégicas mais eficientes e adaptar suas estratégias com base nas escolhas e resultados passados. Dessa forma, as empresas podem ajustar gradualmente suas ações para obter melhores resultados e alcançar equilíbrios de longo prazo em um ambiente competitivo.
Este tutorial tem como objetivo ensinar como aplicar a teoria dos jogos no ambiente R, utilizando o pacote Rgamer, desenvolvido por Yusei Yanai, Ph.D. em Ciência Política, e Yoshio Kamijo, Especialista em Economia Experimental, Teoria dos Jogos, Teoria Comportamental dos Jogos e Design do Futuro. Desse modo, através da integração de funções de modelos de aprendizado, exploraremos a teoria dos jogos e sua aplicação prática. O pacote oferece representações visuais de jogos para dois ou mais jogadores e possibilita encontrar equilíbrios de Nash, proporcionando uma compreensão mais profunda dos conceitos fundamentais no contexto das Ciências Econômicas. Com o Rgamer, tem-se disponível uma ferramenta poderosa para a análise e simulação de interações estratégicas, tornando o estudo do assunto ainda mais acessível e abrangente.
Pacotes
Para realização dos passos seguintes, será necessário a instalação e ativação do pacote:
# install.packages("devtools")
# devtools::install_github("yukiyanai/rgamer")
library(rgamer)
library(utf8)
Jogos Simultâneos
Os jogos simultâneos representam uma categoria fundamental na teoria dos jogos, na qual todos os jogadores tomam suas decisões ao mesmo tempo, sem qualquer conhecimento prévio das escolhas dos outros jogadores. No ambiente de programação R, o pacote Rgamer oferece uma ampla gama de recursos que facilitam a modelagem de jogos simultâneos, o cálculo de equilíbrios de Nash, a representação gráfica e a análise de estratégias dominantes.
Estratégias Puras
O dilema dos prisioneiros é um clássico exemplo de jogo de estratégia pura em teoria dos jogos que envolve dois jogadores que enfrentam uma escolha difícil entre cooperar ou trair o outro jogador. Através da função normal_form() teremos dois exemplos desse tipo forma normal de jogo em dois métodos.
Neste primeiro método, é necessário definir os pagamentos para cada célula da matriz do jogo utilizando o argumento cells, que é configurado como uma lista, no caso list(). Também é necessário especificar os jogadores, que, neste exemplo, são "Bonnie" e "Clyde", utilizando o argumento players, em que as estratégias, "Confessar" e "Não Confessar", respectivamente, são definidas nos argumentos s1 e s2 para eles.
O argumento lógico byrow pode ser configurado como TRUE ou FALSE. Quando definido como TRUE, os valores na lista dentro das células são especificados por linha, seguindo a ordem das estratégias “Confessar” e “Não Confessar”, respectivamente, para cada jogador. Se configurado como FALSE, os valores serão organizados por coluna.
jogo1 <- normal_form(
players = c("Bonnie", "Clyde"),
s1 = c("Confessar", "Não Confessar"),
s2 = c("Confessar", "Não Confessar"),
cells = list(c(-8, -8),
c(0, -15),
c(-15, 0),
c(-1, -1)),
byrow = TRUE)
Para encontrar a solução do primeiro método é necessário a função solve_nfg() e o argumento show_table = TRUE para obter a tabela e o equilíbrio de Nash.
s_jogo1 <- solve_nfg(jogo1, show_table = TRUE)
Pure-strategy NE: [Confessar, Confessar]
|
Clyde
|
|||
|---|---|---|---|
| strategy | Confessar | Não Confessar | |
| Bonnie | Confessar | -8^, -8^ | 0^, -15 |
| Não Confessar | -15, 0^ | -1, -1 | |
Considerando o fator “traição”, escolher confessar é sempre a melhor opção para Bonnie, independentemente da escolha de Clyde. A estratégia de não confessar pode levar a resultados piores se o outro jogador escolher confessar. Portanto, confessar é a estratégia dominante para ambos, incentivando a cooperação mútua.
Estratégias Dominantes
As estratégias estritamente dominantes referem-se a uma situação em que um jogador tem uma estratégia que é sempre melhor do que qualquer outra estratégia que ele possa escolher, independentemente das escolhas dos outros jogadores.
No exemplo a seguir, os jogadores "Pedro" e "Ana" são especificados no argumento players. Neste jogo, ao contrário dos dois exemplos anteriores, cada jogador possui 3 estratégias disponíveis: "Bar", "Museu" e "Café". Dessa forma, será necessário aumentar o número de elementos nas matrizes payoffs1 e payoffs2, agora contendo um total de 9 elementos.
jogo3 <- normal_form(
players = c("Pedro", "Ana"),
s1 = c("Bar", "Museu", "Café"),
s2 = c("Bar", "Museu", "Café"),
payoffs1 = c(6, 2, 1,
6, 5, 1,
4, 2, 3),
payoffs2 = c(4, 1, 1,
3, 5, 3,
2, 2, 6))
O argumento lógico mark_br desempenha a função de destacar as melhores respostas (best responses) na tabela de solução. Quando é definido como FALSE, as melhores respostas não são destacadas na tabela. O valor padrão para mark_br é TRUE, o que significa que, caso esse argumento na função não seja incluído na função, a tabela exibirá automaticamente o equilíbrio de Nash.
Nesse caso, o equilíbrio de Nash em conjunto com a mensagem não serão exibidas, já que ao configurar quietly como TRUE, está sendo implicitamente ocultado a mensagem de melhores respostas. Essa configuração flexível permite controlar tanto a exibição da mensagem quanto o destaque do Equilíbrio de Nash, de acordo com as preferências.
s_jogo3 <- solve_nfg(jogo3,
show_table = TRUE,
mark_br = FALSE,
quietly = TRUE)
Ana |
||||
|---|---|---|---|---|
| strategy | Bar | Museu | Café | |
| Pedro | Bar | 6, 4 | 6, 3 | 4, 2 |
| Museu | 2, 1 | 5, 5 | 2, 2 | |
| Café | 1, 1 | 1, 3 | 3, 6 | |
Na função dom() com type = "dominant", são identificadas as estratégias estritamente dominantes para cada jogador no jogo. Por meio dessa configuração é possível identificar as estratégias que são sempre a melhor escolha, independentemente das ações tomadas pelos outros jogadores.
Diferentemente do parâmetro quietly encontrado em funções como solve_nfg() e outras do pacote Rgamer, é essencial demonstrar que ao configurar esse parâmetro como FALSE na função dom(), ela passa a exibir uma mensagem que identifica quais estratégias são estritamente dominantes.
dominant_j3 <- dom(jogo3,
type = "dominant",
quietly = FALSE)
Pedro's dominant strategy: Bar
Pedro's weakly dominant strategy: Bar
Ana's dominant strategy: NA
Ana's weakly dominant strategy: NA
No primeiro conjunto de resultados, ao analisar as estratégias estritamente dominantes, identificamos que a estratégia “Bar” é a melhor resposta para Pedro. Nesse contexto, essa estratégia é a escolha que Pedro deve realizar independentemente das escolhas de Ana.
Contudo, é importante ressaltar que a existência de estratégias estritamente dominantes em jogos não é uma característica universal, variando conforme as regras e as interações específicas dentro de cada jogo. Desse modo, quando tais estratégias estão presentes, elas desempenham um papel crucial na análise e na formulação de decisões estratégicas.
Estratégias Dominadas
A dominância fraca é um dos critérios usados para identificar estratégias não razoáveis ou não ótimas em um jogo. Ela indica a existência de outra estratégia que é, no mínimo, tão boa quanto a estratégia dominada fracamente, mas que pode oferecer um melhor resultado em algumas situações específicas.
No mesmo exemplo, faremos uma alteração no parâmetro type, em que anteriormente estava definido como "dominant", mas agora será configurado como "dominated". O objetivo dessa modificação é identificar estratégias que são dominadas e fracamente dominadas tanto para Pedro quanto para Ana.
dominated_j3 <- dom(jogo3,
type = "dominated",
quietly = FALSE)
Pedro's dominated strategy: Museu, Café
Pedro's weakly dominated strategy: Museu, Café
Ana's dominated strategy: NA
Ana's weakly dominated strategy: NA
Através da análise do segundo conjunto, podemos evidenciar que para o jogador Pedro, as estratégias “Museu” e “Café” são dominadas por outra estratégia, pois sempre há uma escolha alternativa, no caso “Bar”, que leva a um resultado melhor, independentemente da escolha do outro jogador.
Na perspectiva de Ana, em ambos os conjuntos de resultados, não foram encontradas estratégias dominadas nem dominantes, o que indica que suas escolhas são consideradas melhores respostas dadas as escolhas de Pedro.
br_j3 <- solve_nfg(jogo3)
Pure-strategy NE: [Bar, Bar]
Ana |
||||
|---|---|---|---|---|
| strategy | Bar | Museu | Café | |
| Pedro | Bar | 6^, 4^ | 6^, 3 | 4^, 2 |
| Museu | 2, 1 | 5, 5^ | 2, 2 | |
| Café | 1, 1 | 1, 3 | 3, 6^ | |
Agora, ao verificar as melhores estratégias para o jogador 1 e 2, a mensagem e o destaque do Equilíbrio de Nash podem ser exibidos. Dentro da estrutura da função solve_nfg(), ao remover o parâmetro show_table, a tabela será exibida por padrão, assim como ocorre com outros parâmetros como quietly e mark_br.
Estratégias Mistas
Imagine um cenário onde o Governo e uma pessoa pobre estão interagindo. O Governo tem duas estratégias possíveis: “Ajuda” e “Não Ajuda”, enquanto a pessoa pobre tem duas estratégias: “Trabalha” e “Vadia”.
jogo4 <- normal_form(
players = c("Governo", "Pobre"),
s1 = c("Ajuda", "Não Ajuda"),
s2 = c("Trabalha", "Vadia"),
payoffs1 = c(3, -1, -1, 0),
payoffs2 = c(2, 1, 3, 0))
Nesse jogo, o Governo e o pobre podem optar por estratégias puras, ou seja, escolher uma ação específica com certeza, ou podem utilizar estratégias mistas, ou seja, fazer escolhas ponderadas com base em probabilidades. Através do parâmetro mixed = TRUE, podemos encontrar a solução para esse tipo de jogo para as estratégias mistas.
s_jogo4 <- solve_nfg(jogo4,
mixed = TRUE,
show_table = FALSE)
Pure strategy NE does not exist.
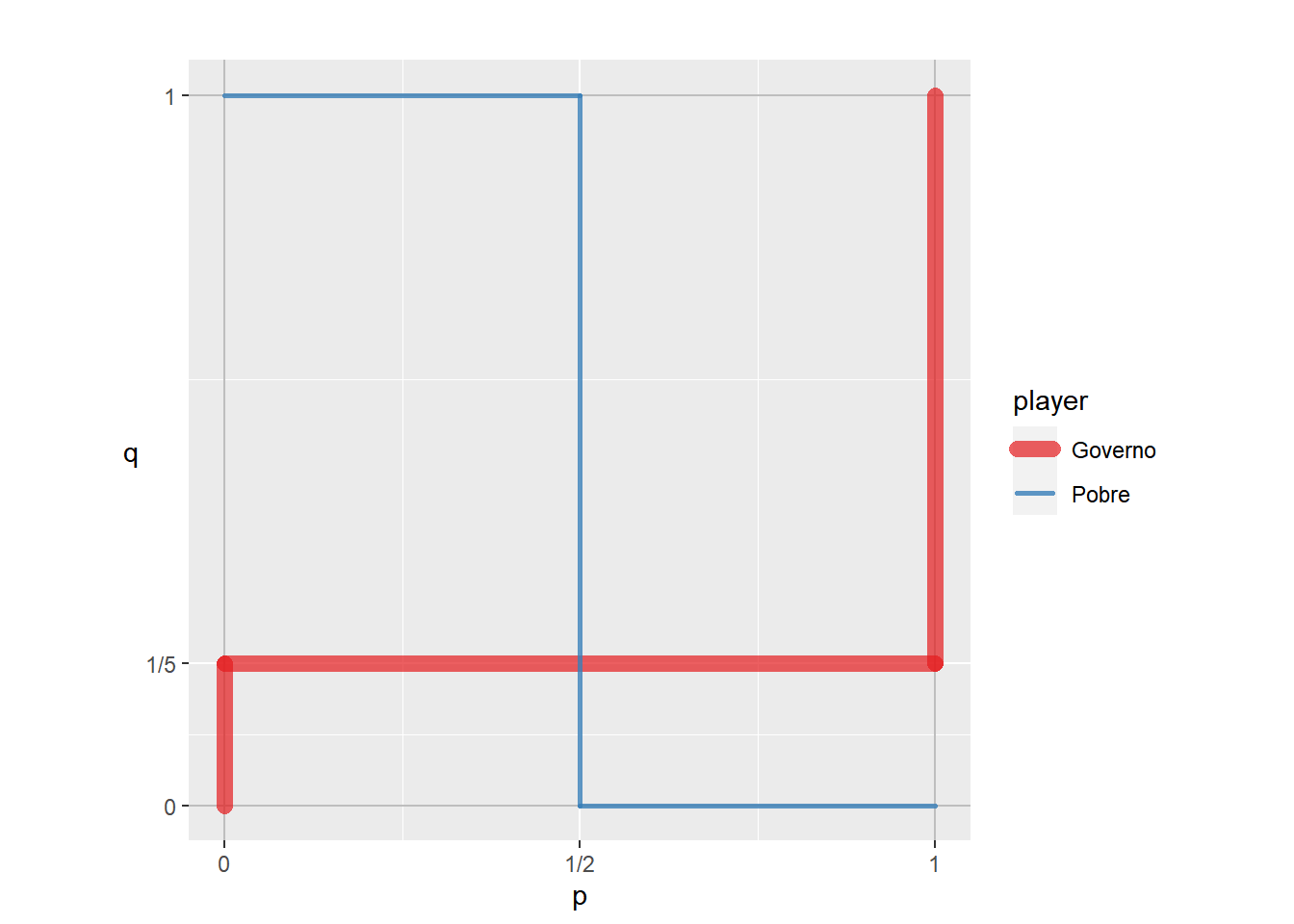
Mixed-strategy NE: [(1/2, 1/2), (1/5, 4/5)]
The obtained mixed-strategy NE might be only a part of the solutions.
Please examine br_plot (best response plot) carefully.
Com a função br_plot (best response plot) ou gráfico de melhores respostas é possível se chegar a maximização do payoff esperado.
s_jogo4$br_plot
A função de payoff em estratégias mistas é usada para representar o resultado esperado que um jogador obtém ao escolher uma determinada ação com probabilidade ou com incerteza. No exemplo a seguir estão as funções de payoff para as estratégias dos jogadores A e B.
-
Jogador: $\{A, B\}$
-
Estratégia: $\{x \in [0, 1], y \in [0, 1] \}$
-
Payoff: $\{f_x(x, y) = -3x^2 + (1 - y) \times 2x, f_y(x, y) = -2y^2 + (1 - x) \times 3y\}$
Desse modo, é possível definir um jogo fornecendo as funções de payoff como vetores de caracteres usando a função normal_form(). Nos parâmetros par1_lim e par2_lim estão configurados os valores entre 0 e 1, o que significa que as estratégias ou escolhas dos jogadores “A” e “B” estão limitadas a esse intervalo. Esses argumentos definem os limites para os eixos, no caso, "x" e "y" contidas em pars.
jogo5 <- normal_form(
players = c("A", "B"),
payoffs1 = "-4*x^2 + (1-y) * 2*x",
payoffs2 = "-2*y^2 + (1-x) * 3*y",
par1_lim = c(0, 1),
par2_lim = c(0, 1),
pars = c("x", "y"))
Com a construção da estrutura do jogo na forma normal, temos a solução dele a apartir da função solve_nfg().
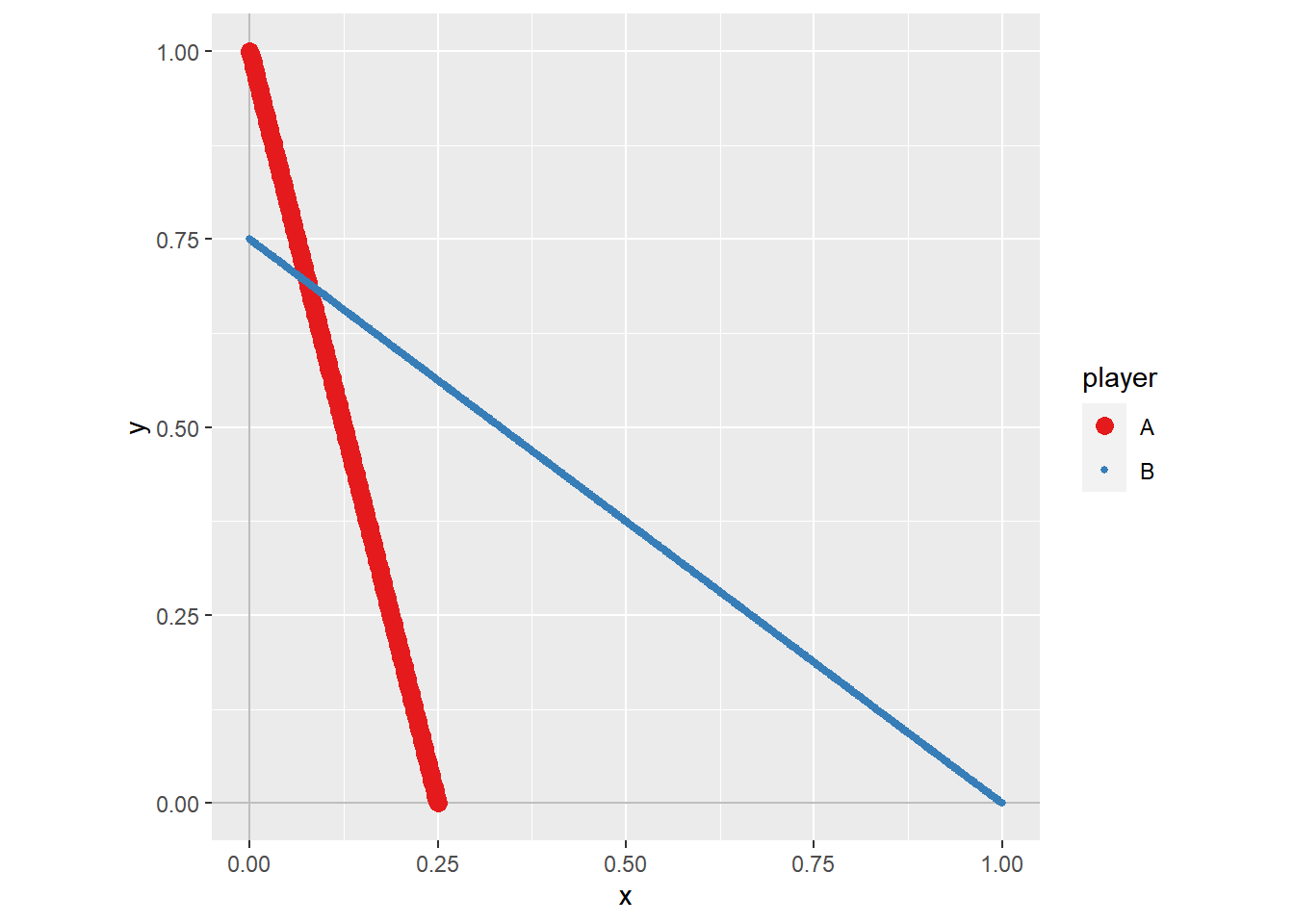
s_jogo5 <- solve_nfg(jogo5)
approximated NE: (0.1, 0.7)
The obtained NE might be only a part of the solutions.
Please examine br_plot (best response plot) carefully.
Nesse método alternativo, é possível definir os resultados de um jogo na forma normal, utilizando function da linguagem R
-
Jogador: $\{A, B\}$
-
Estratégia: $\{x \in [0, 1], y \in [0, 1] \}$
-
Payoff: $\{f_x(x, y) = -nx^a + (b - y) \times px, f_y(x, y) = -my^s + (t - x) \times qy\}$
# Função do jogador 1
f_x <- function(x, y, a, b, n, p) {
-n*x^a + (b - y) * p*x
}
# Função do jogador 2
f_y <- function(x, y, s, t, m, q) {
-m*y^s + (t - x) * q*y
}
Após a definição das funções para os jogadores 1 e 2, podemos incorporá-las dentro da normal_form() nos parâmetros payoffs1 e payoffs2.
jogo6 <- normal_form(
players = c("A", "B"),
payoffs1 = f_x,
payoffs2 = f_y,
par1_lim = c(0, 1),
par2_lim = c(0, 1),
pars = c("x", "y"))
Para obter uma solução aproximada numericamente usando o solve_nfg(), é necessário definir os valores dos parâmetros da função que devem ser tratados como constantes, utilizando os argumentos cons1 e cons2, ambos aceitando uma lista de nomes. Além disso, é possível evitar que o gráfico das melhores respostas seja exibido, definindo plot = FALSE.
spf_jogo6 <- solve_nfg(
game = jogo6,
cons1 = list(
a = 2, b = 1, n = 4, p = 2
),
cons2 = list(
s = 2, t = 1, m = 2, q = 3
),
plot = FALSE)
## approximated NE: (0.1, 0.7)
## The obtained NE might be only a part of the solutions.
## Please examine br_plot (best response plot) carefully.
É possível ajustar a precisão da aproximação através do parâmetro precision (por padrão, precision = 1). Ao aumentar o valor, o cálculo das soluções será feito com maior detalhamento, resultando em uma aproximação mais precisa dos resultados. No entanto, é importante notar que quanto maior o valor desse parâmetro, mais tempo o processo de cálculo pode levar, especialmente para jogos mais complexos com muitas estratégias e jogadores. Portanto, é recomendado ajustar o valor da precisão de acordo com a complexidade do jogo e a necessidade de precisão dos resultados.
s_jogo6 <- solve_nfg(
game = jogo6,
cons1 = list(
a = 2, b = 1, n = 4, p = 2
),
cons2 = list(
s = 2, t = 1, m = 2, q = 3
),
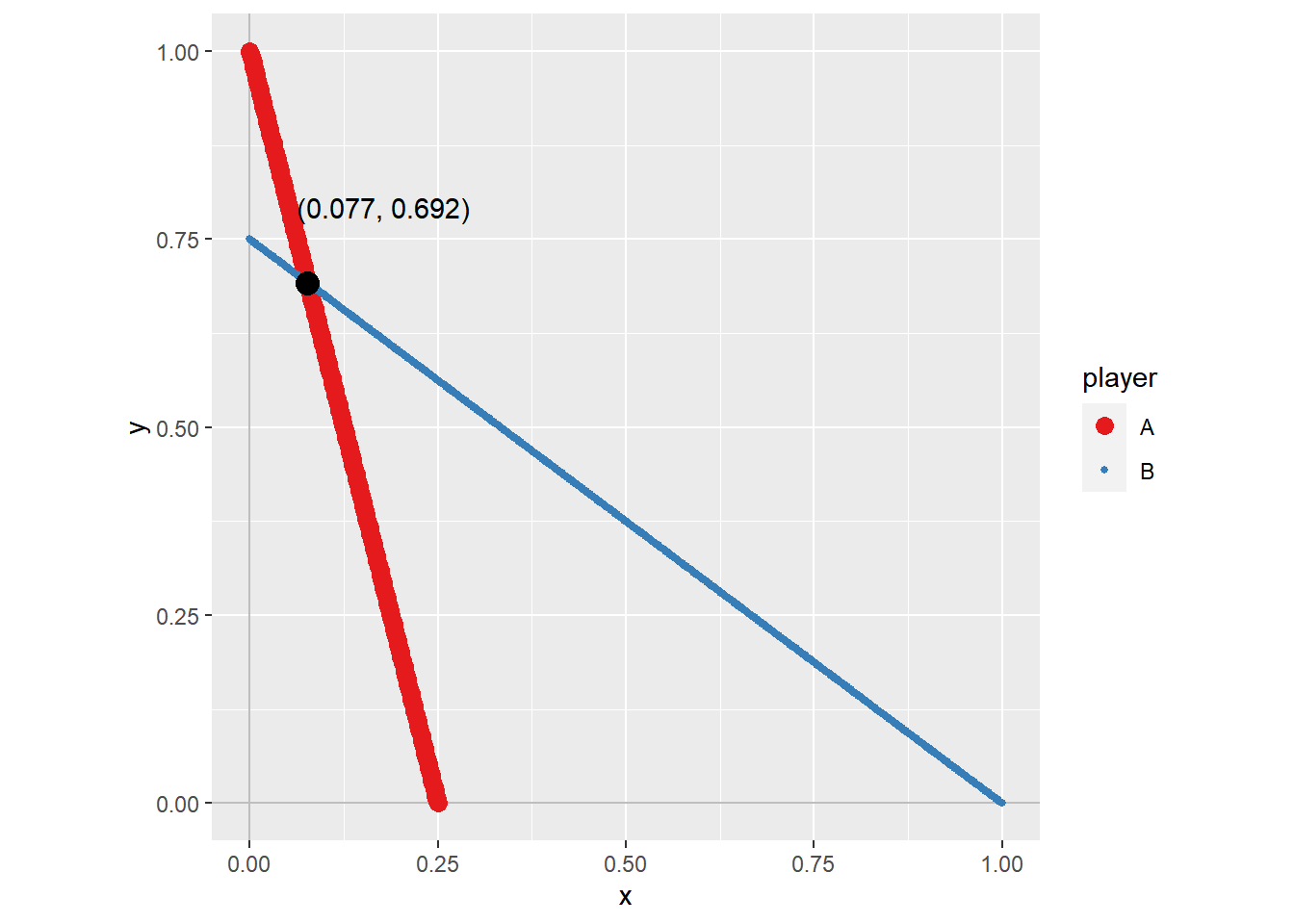
precision = 3)
approximated NE: (0.077, 0.692)
The obtained NE might be only a part of the solutions.
Please examine br_plot (best response plot) carefully.
Para extrair o gráfico das melhores respostas com o ponto de Equilíbrio de Nash (NE) marcado, é possível utilizar a função br_plot_NE. Esse gráfico mostra como as estratégias dos jogadores podem mudar e se adaptar para alcançar o NE.
s_jogo6$br_plot_NE
Com estratégias mistas, os jogadores podem tomar decisões aleatórias com diferentes probabilidades para cada ação. Isso torna o resultado do jogo mais incerto, pois o desfecho dependerá das escolhas aleatórias feitas por cada jogador.
Outros Exemplos
Neste jogo, duas empresas, a “Empresa A” e a “Empresa B”, participam de uma disputa para ganhar um contrato. Cada uma delas deve escolher um lance entre 1 e 10 milhões de reais.
-
Se a “Empresa A” fizer o lance mais alto, ela ganha o contrato e recebe uma recompensa de 10 milhões. Enquanto isso, a “Empresa B” não ganha o contrato e ela acaba tendo prejuízo de 1 milhão.
-
Por outro lado, se a “Empresa A” fizer o lance mais alto, ela ganha o contrato e recebe a recompensa de 10 milhões. Enquanto isso, a “Empresa B” não ganha o contrato e perde 1 milhão.
-
Se ambas as empresas fizerem exatamente o mesmo lance, elas não conseguem diferenciar suas ofertas, e o contrato é anulado. Nesse caso, nenhuma das empresas recebe a recompensa.
Com base no exemplo mencionado anteriormente, utilizaremos novamente a palavra-chave function do R para representar a função de payoff. Isso se deve ao maior espaço estratégico presente no jogo, o qual possibilita mais combinações de lances e, por consequência, mais resultados em comparação com o jogo do dilema dos prisioneiros.
# Payoff do jogador 1
func_payoff1 <- function(a, b) {
if (a < b) {
profit <- -1
} else if (a == b) {
profit <- 0
} else {
profit <- 10
}
profit
}
# Payoff do jogador 2
func_payoff2 <- function(a, b){
if (a > b) {
profit <- -1
} else if (a == b) {
profit <- 0
} else {
profit <- 10
}
profit
}
Após a definição das funções de payoff, podemos passar o exemplo acima para a função normal_form(), utilizando as condições de func_payoff1 e func_payoff2.
jogo11 <- normal_form(
players = c("Empresa A",
"Empresa B"),
payoffs1 = func_payoff1,
payoffs2 = func_payoff2,
pars = c("a", "b"),
s1 = c(seq(1, 10,1)),
s2 = c(seq(1, 10,1)),
discretize = TRUE)
A opção discretize = TRUE é usada quando o conjunto contínuo de estratégias é muito grande, tornando a avaliação completa computacionalmente custosa. Nesse caso, o jogo é avaliado apenas em um conjunto específico de pontos discretos, em vez de considerar todas as combinações possíveis de estratégias contínuas. O padrão é discretize = FALSE, que significa que o jogo é avaliado considerando todas as possíveis combinações contínuas de estratégias.
Nesse contexto, na função solve_nfg(), o parâmetro mark_br será definido como FALSE, uma vez que não haverá marcação das melhores respostas para cada estratégia do oponente, devido à consideração restrita a pontos discretos ao invés de todas as combinações contínuas de estratégias.
s_jogo11 <- solve_nfg(jogo11, mark_br = FALSE)
Pure-strategy NE: [10, 10]
Empresa B |
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| strategy | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| Empresa A | 1 | 0, 0 | -1, 10 | -1, 10 | -1, 10 | -1, 10 | -1, 10 | -1, 10 | -1, 10 | -1, 10 | -1, 10 |
| 2 | 10, -1 | 0, 0 | -1, 10 | -1, 10 | -1, 10 | -1, 10 | -1, 10 | -1, 10 | -1, 10 | -1, 10 | |
| 3 | 10, -1 | 10, -1 | 0, 0 | -1, 10 | -1, 10 | -1, 10 | -1, 10 | -1, 10 | -1, 10 | -1, 10 | |
| 4 | 10, -1 | 10, -1 | 10, -1 | 0, 0 | -1, 10 | -1, 10 | -1, 10 | -1, 10 | -1, 10 | -1, 10 | |
| 5 | 10, -1 | 10, -1 | 10, -1 | 10, -1 | 0, 0 | -1, 10 | -1, 10 | -1, 10 | -1, 10 | -1, 10 | |
| 6 | 10, -1 | 10, -1 | 10, -1 | 10, -1 | 10, -1 | 0, 0 | -1, 10 | -1, 10 | -1, 10 | -1, 10 | |
| 7 | 10, -1 | 10, -1 | 10, -1 | 10, -1 | 10, -1 | 10, -1 | 0, 0 | -1, 10 | -1, 10 | -1, 10 | |
| 8 | 10, -1 | 10, -1 | 10, -1 | 10, -1 | 10, -1 | 10, -1 | 10, -1 | 0, 0 | -1, 10 | -1, 10 | |
| 9 | 10, -1 | 10, -1 | 10, -1 | 10, -1 | 10, -1 | 10, -1 | 10, -1 | 10, -1 | 0, 0 | -1, 10 | |
| 10 | 10, -1 | 10, -1 | 10, -1 | 10, -1 | 10, -1 | 10, -1 | 10, -1 | 10, -1 | 10, -1 | 0, 0 | |
A Batalha dos Sexos é um exemplo clássico na teoria dos jogos que ilustra a situação em que dois jogadores têm preferências diferentes, mas desejam coordenar suas ações. Neste exemplo, consideramos um casal composto por um homem e uma mulher que precisam decidir entre duas atividades: assistir a um jogo de futebol ou assistir a um balé.
Suponha que o marido prefira assistir a um jogo de futebol, enquanto a esposa prefira assistir a um balé. No entanto, ambos preferem estar juntos do que fazer atividades separadas. Portanto, eles precisam chegar a um acordo sobre qual evento assistir juntos.
jogo12 <- normal_form(
players = c("Marido", "Esposa"),
s1 = c("Futebol(p)", "Balé(1-p)"),
s2 = c("Futebol(q)", "Balé(1-q)"),
payoffs1 = c(10, 1, 2, 5),
payoffs2 = c(6, 2, 3, 10))
# Transformando o jogo 12 em tabela
table_jogo12 <- solve_nfg(jogo12,
show_table = TRUE,
mark_br = FALSE)
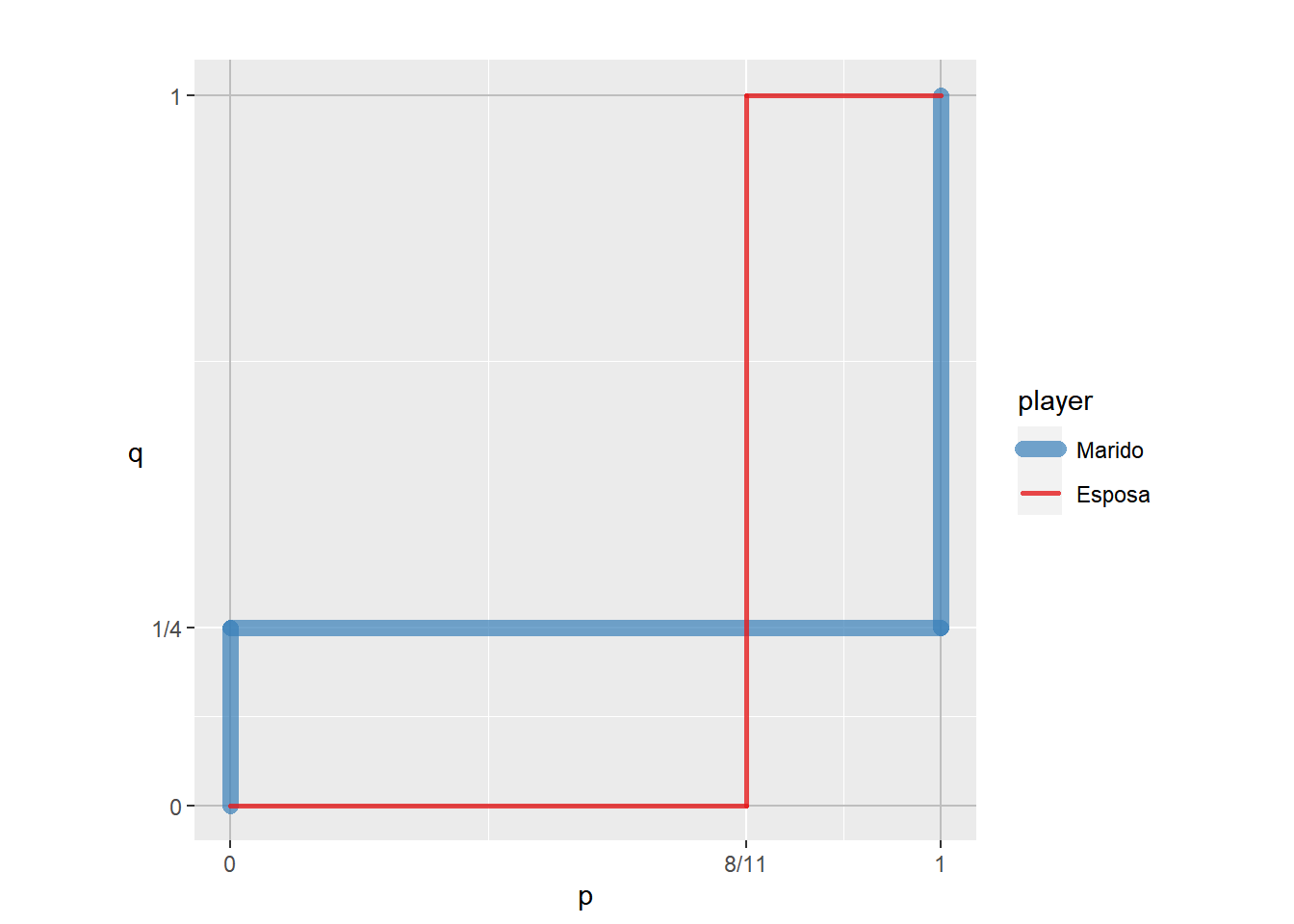
Pure-strategy NE: [Futebol(p), Futebol(q)], [Balé(1-p), Balé(1-q)]
Esposa |
|||
|---|---|---|---|
| strategy | Futebol(q) | Balé(1-q) | |
| Marido | Futebol(p) | 10, 6 | 2, 3 |
| Balé(1-p) | 1, 2 | 5, 10 | |
A utilidade esperada dos dois é calculada com base na fórmula que leva em conta as probabilidades $p$ e $q$ presentes na tabela acima. Simplificamos e combinamos os termos para obter o resultado da utilidade esperada.
$E(U_{M}) = 10pq + 2p(1 - q) + 1(1 - p)q + 5(1 - p)(1 - q)$
$E(U_{M}) = 10pq + 2p - 2pq + q - pq + 5 - 5p - 5q + 5pq$
$E(U_{M}) = 12pq - 4q - 3p + 5$
${\large{\frac{\partial U_{M}}{\partial p}}} = 12pq - 4q - 3p + 5$
Para encontrar o valor de $q$ que maximiza a utilidade esperada do marido, igualamos a derivada parcial em relação a $q$ a zero:
$12q - 3 = 0$
$q = \frac{1}{4}$
Com base na resposta anterior, pode-se usar a mesma lógica para calcular a utilidade esperada da esposa.
$E(U_{E}) = 6pq + 3p(1-q) + 2(1-p)q + 10(1-p)(1-q)$
$E(U_{E}) = 6pq + 3p - 3pq + 2q - 2pq + 10 - 10p - 10q + 10pq$
$E(U_{E}) = 11pq - 7p - 8q + 10$
${\large{\frac{\partial U_{E}}{\partial q}}} = 11pq - 7p - 8q + 10$
Para encontrar o valor de $p$ que maximiza a utilidade esperada, igualamos a derivada parcial em relação a $p$ a zero:
$11p - 8 = 0$
$p = \frac{8}{11}$
O resultado da utilidade esperada do casal pode ser visualizado de forma gráfica utilizando a função br_plot.
table_jogo12$br_plot
Referências
MANKIW, N. Gregory et al. Introdução à economia. 2005.
YANAI, Yusei; KAMIJO, Yoshio. Game Theory With R. Shin-Ogawacho, Shinjuku-ku, Tóquio, JP: Asakura Publishing Co,. Ltd., 2023. 244 p. ISBN 978-4-254-27024-2 C3050.
