Introdução
Se você ainda não conferiu nosso tutorial sobre Teoria dos Jogos no R, abordando Jogos Simultâneos, clique aqui para acessar diretamente o post.
Pacotes
Para realização dos passos seguintes, será necessário a instalação e ativação do pacote:
# install.packages("devtools")
# devtools::install_github("yukiyanai/rgamer")
library(rgamer)
library(utf8)
Jogos Sequenciais
Jogos sequenciais são modelos que representam a tomada de decisão em sequência, levando em conta as escolhas dos jogadores e as informações disponíveis. A análise desses jogos envolve a busca por estratégias ótimas e a previsão dos desdobramentos com base nessas estratégias. Na aplicação de jogos sequenciais no R, há funções que auxiliam na construção gráfica da forma extensiva e sequencial do jogo.
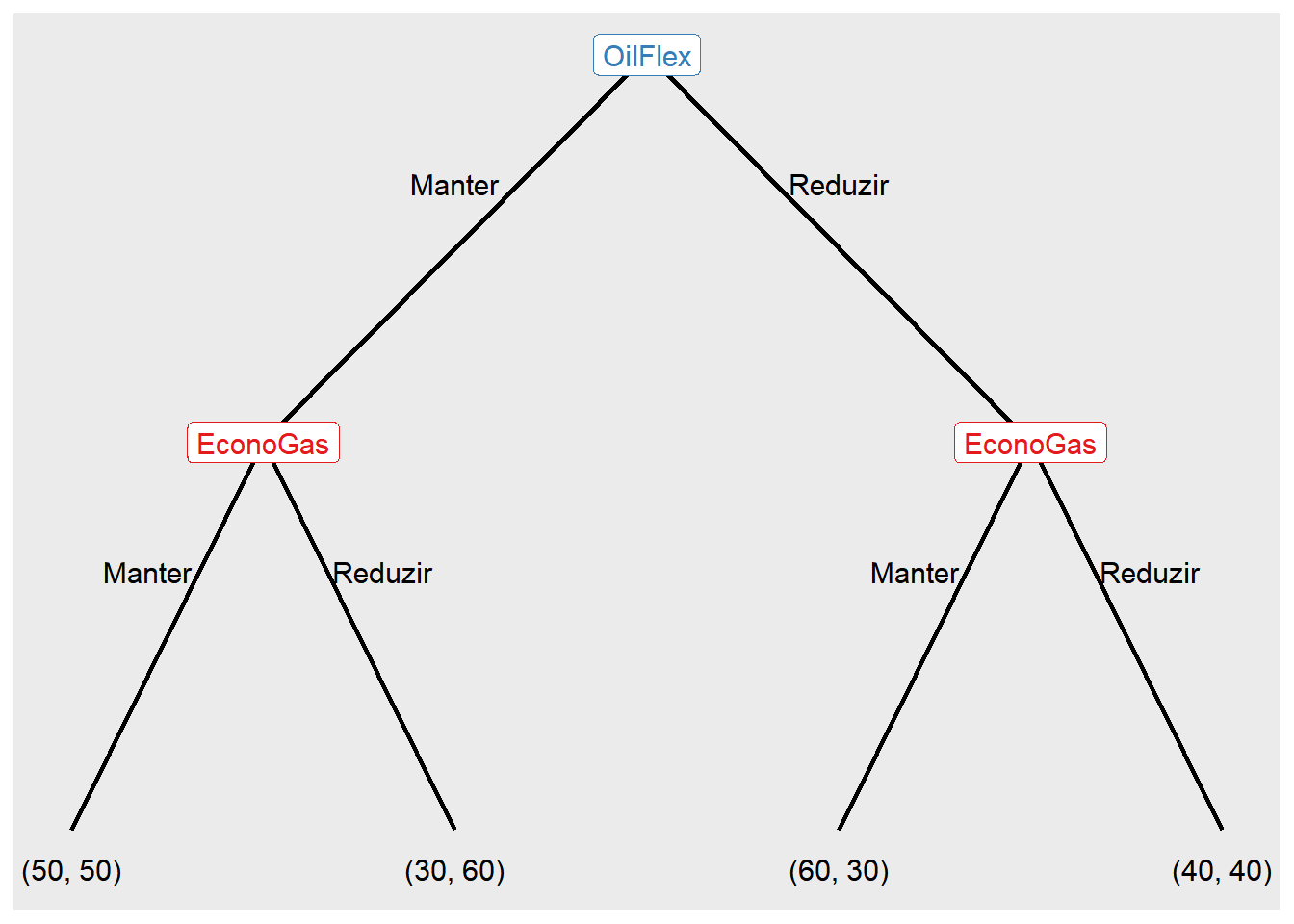
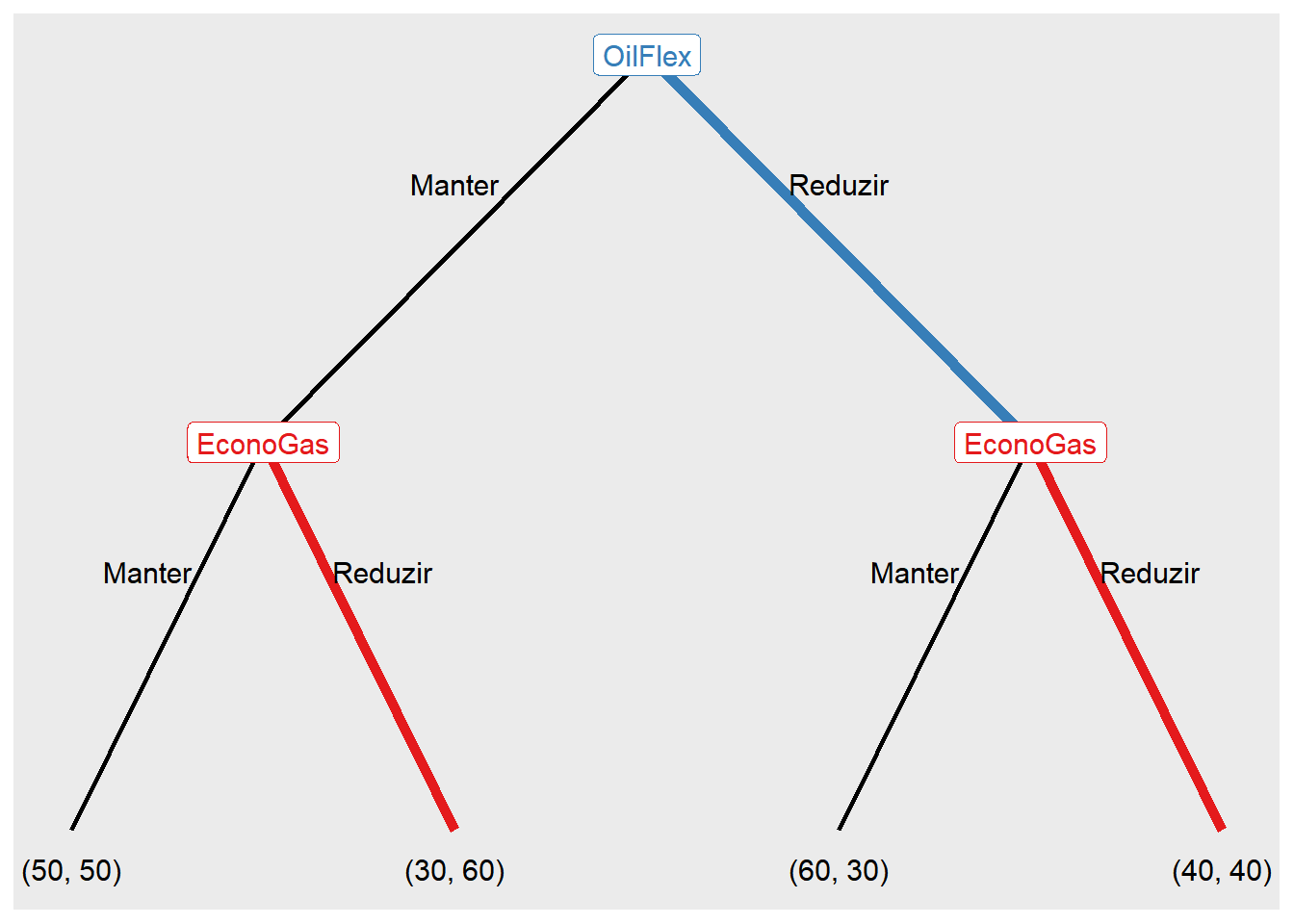
Na representação extensiva, podemos utilizar o exemplo mencionado anteriormente da guerra de preços entre dois postos de gasolina. Nessa estrutura de jogo, ao contrário da forma normal, os jogadores tomam decisões em uma ordem específica. Começando com o posto “OilFlex”, que é o jogador inicial e tem um nó na árvore de decisão, e “EconoGas”, que é repetido duas vezes porque possui dois nós, um para cada situação em que pode reagir às ações tomadas pelo outro posto de gasolina. Essa diferenciação ocorre porque o jogador inicial, neste caso, começa a árvore de decisão, enquanto o segundo jogador reage a essa ação inicial. O mesmo princípio se aplica às estratégias no argumento actions, que consiste nas estratégias "Manter"" e "Reduzir" para o jogador 1 e 2.
Ao definir rep(NA, 4) dentro do argumento players, estamos indicando que os nós terminais se repetirão quatro vezes, refletindo as possíveis combinações de ações ao longo da árvore de decisão. A estrutura de payoffs é feita em uma lista com o nome dos jogadores, seguida pela especificação de seus ganhos para cada combinação de ações. Essa estrutura, diferentemente da forma normal, é necessária porque a representação extensiva é mais detalhada e explícita, mostrando a árvore de decisão completa do jogo, passo a passo, com informações sobre as ações tomadas em cada nó da árvore. Dessa forma, os payoffs são especificados separadamente para cada jogador em cada nó, permitindo uma representação detalhada das recompensas em cada cenário do jogo.
jogo7 <- extensive_form(
players = list("OilFlex",
c("EconoGas", "EconoGas"),
rep(NA, 4)),
actions = list(c("Manter", "Reduzir"),
c("Manter", "Reduzir"), c("Manter", "Reduzir")),
payoffs = list(OilFlex = c(50, 30, 60, 40),
EconoGas = c(50, 60, 30, 40)),
show_node_id = FALSE)
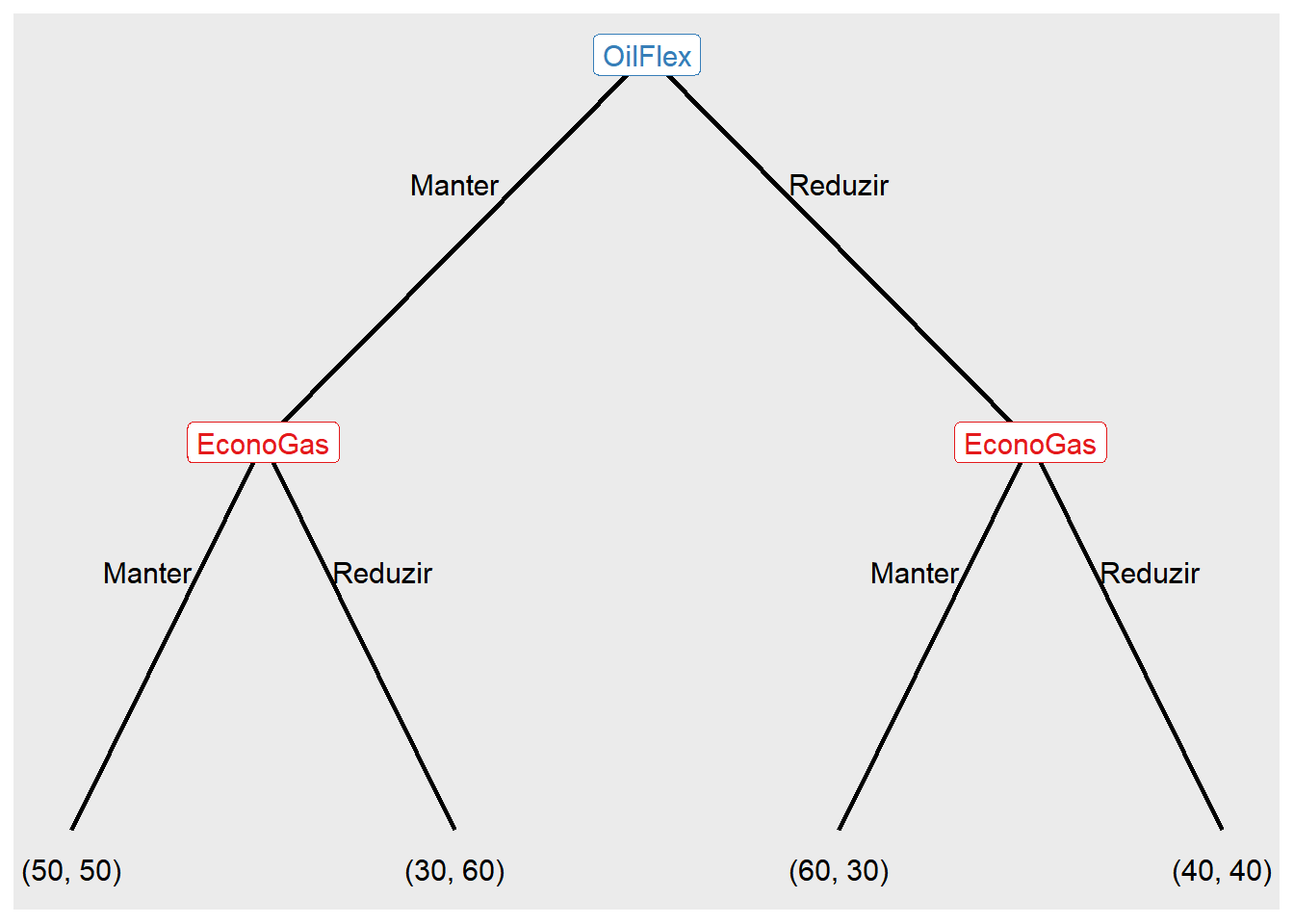
Quando show_node_id é definido como FALSE (sendo TRUE o valor padrão), a árvore de decisões é exibida de maneira simplificada, sem a numeração de cada nó na árvore.
Nesse outro método, iniciamos a estruturação do exemplo utilizando a função seq_form(), o que nos permite especificar as estratégias dos jogadores e os payoffs associados a cada combinação de estratégias.
sq_jogo8 <- seq_form(
players = c("OilFlex", "EconoGas"),
s1 = c("Manter", "Reduzir"),
s2 = c("Manter", "Reduzir"),
payoffs1 = c(50, 60, 30, 40),
payoffs2 = c(50, 30, 60, 40))
A partir disso, usamos a função seq_extensive() para transformar um jogo na forma sequencial, definido com seq_form(), em um jogo na forma extensiva.
jogo8 <- seq_extensive(sq_jogo8,
direction = "right",
color_palette = "Dark2")
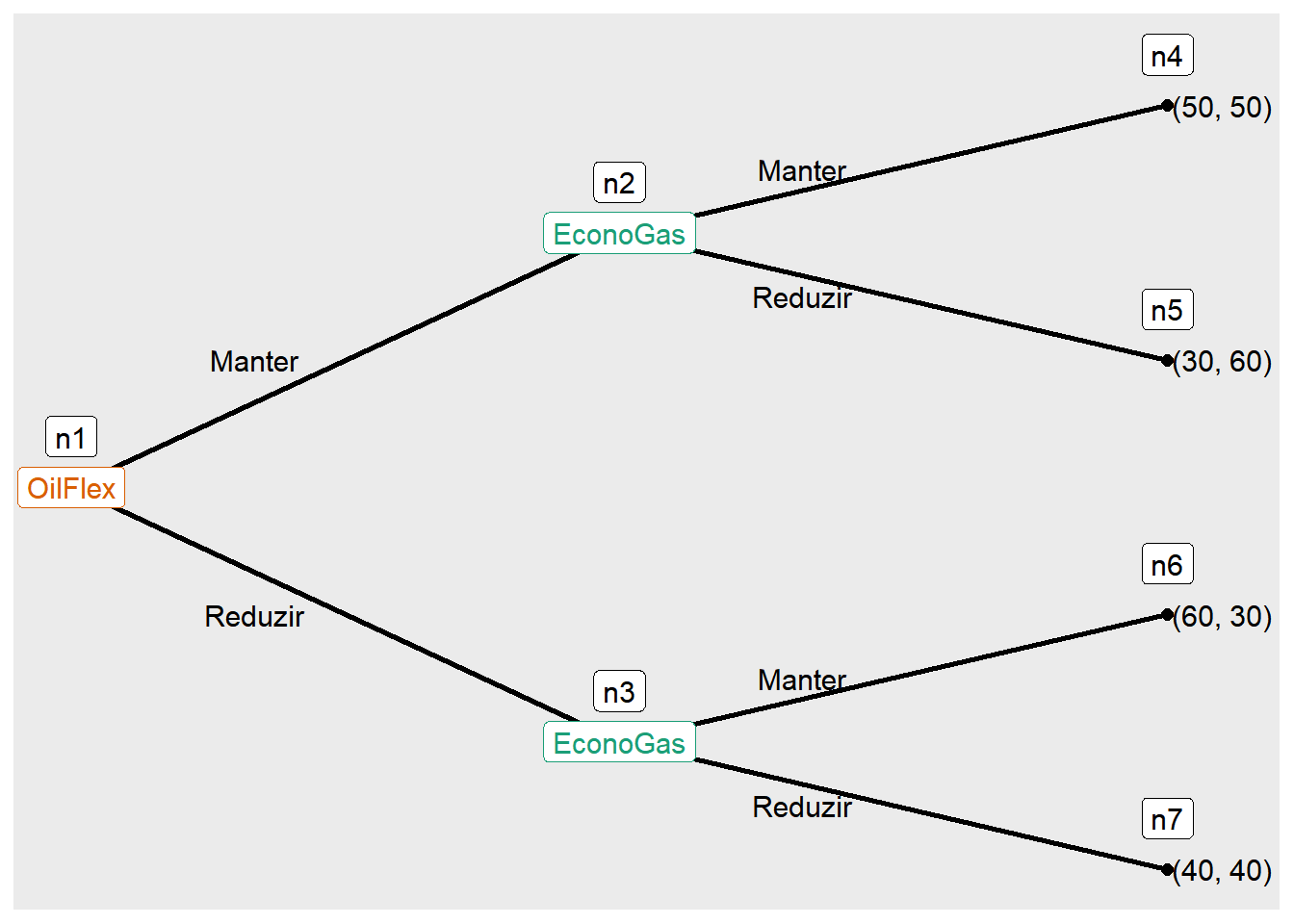
Ao especificarmos o parâmetro direction como "right", a árvore extensiva é direcionada para a direita, e as cores são aplicadas de acordo com a paleta de cores especificada em color_palette.
Além disso, é possível utilizar funções que permitem não somente a indução manual dos caminhos, a restrição das opções dos jogadores, mas também outras funcionalidades que incluem a possibilidade da contagem de subjogos em cada ramo da forma extensiva e a transferência dos dados para matrizes. O que contribui para uma análise mais completa e coerente das possibilidades do jogo.
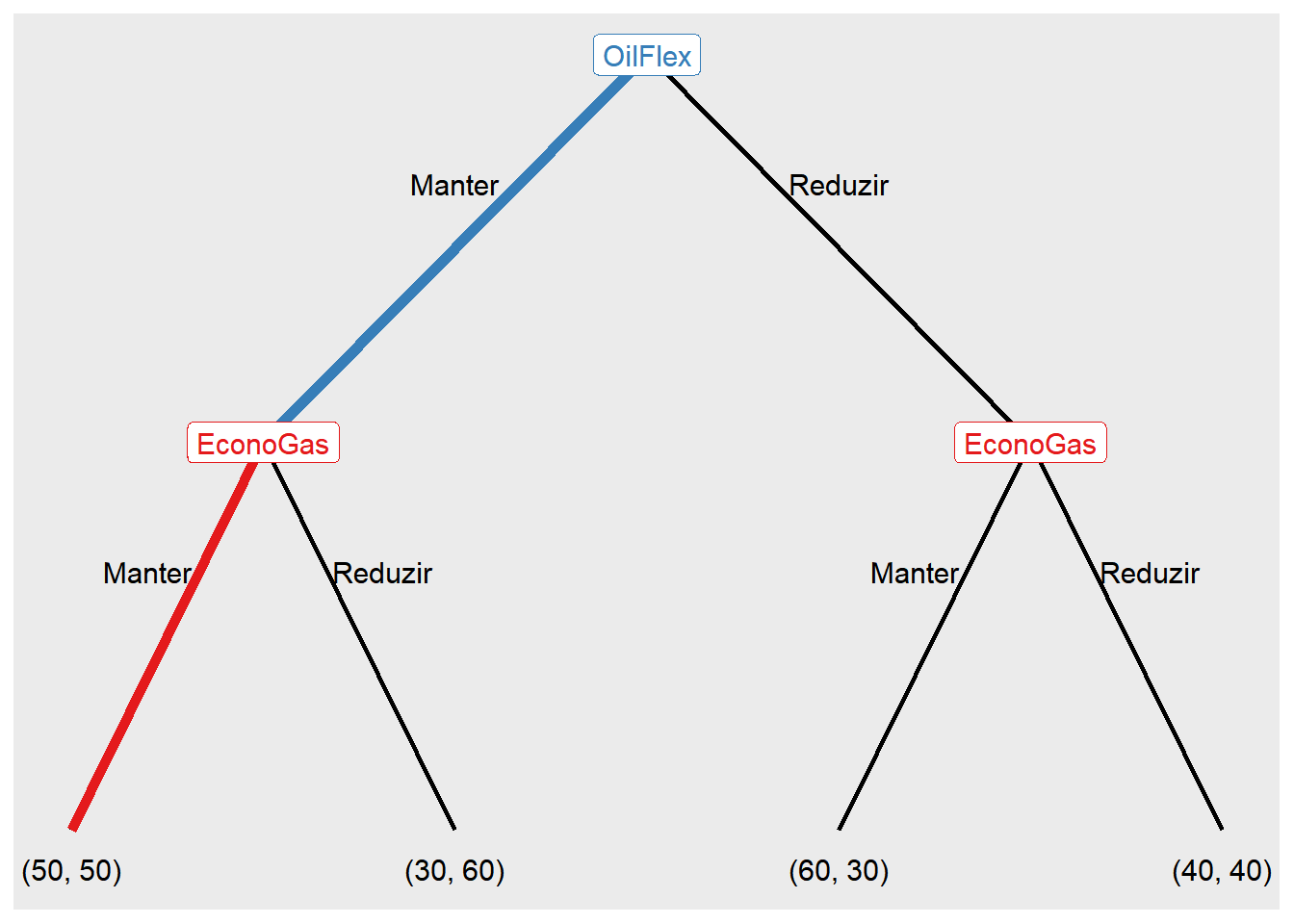
Com a construção da estrutura da forma extensiva, podemos utilizar a função draw_path para induzir os caminhos específicos em um jogo representado em forma de árvore, definido pela função extensive_form().
draw_path(jogo7, actions = list("Manter", "Manter"))
The game reaches at n4.
Payoffs:
OilFlex EconoGas
50 50
The game reaches at n4.
Payoffs:
No R, é possível restringir as ações dos jogadores através da eliminação de certas sequências de jogadas. Essa restrição pode ser feita utilizando o parâmetro actions da função restrict_action(), que recebe uma lista de vetores. Ao utilizar essa função, é possível controlar quais jogadas são permitidas em cada estágio do jogo sequencial.
restrict_action(jogo7, action = list("n1" = "Reduzir",
"n2" = "Reduzir"))
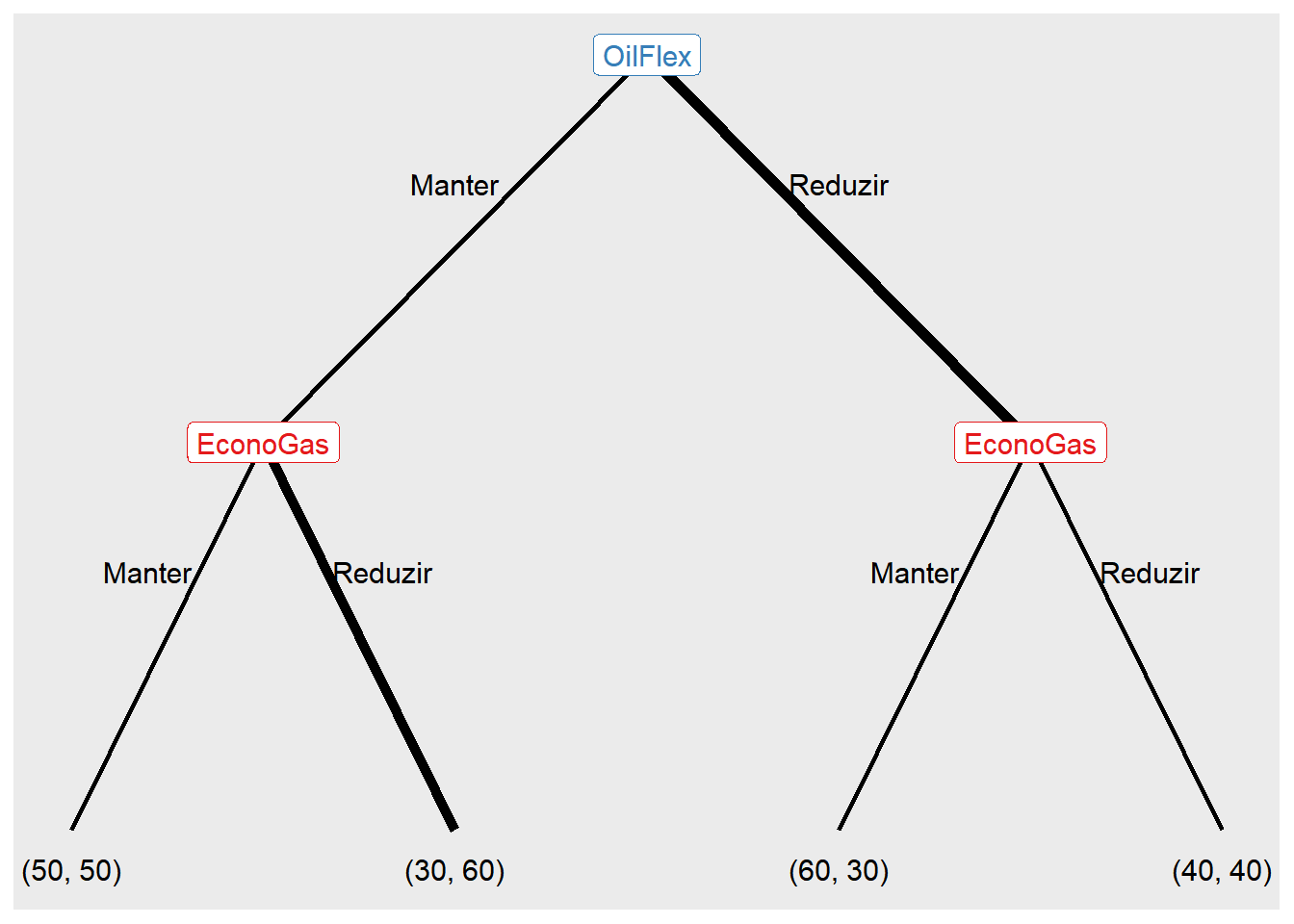
Ao observar o parâmetro action, percebemos que ele contém a identificação dos nós do jogo, neste caso, "n1" e "n2", juntamente com as ações correspondentes, que são "Reduzir" e "Reduzir".
A função subgames() é usada para encontrar e identificar os subjogos dentro de um jogo em forma extensiva. Um subjogo é uma parte do jogo que pode ser analisada e tratada separadamente.
subgames(jogo7, quietly = FALSE)
The game has 3 subgames.
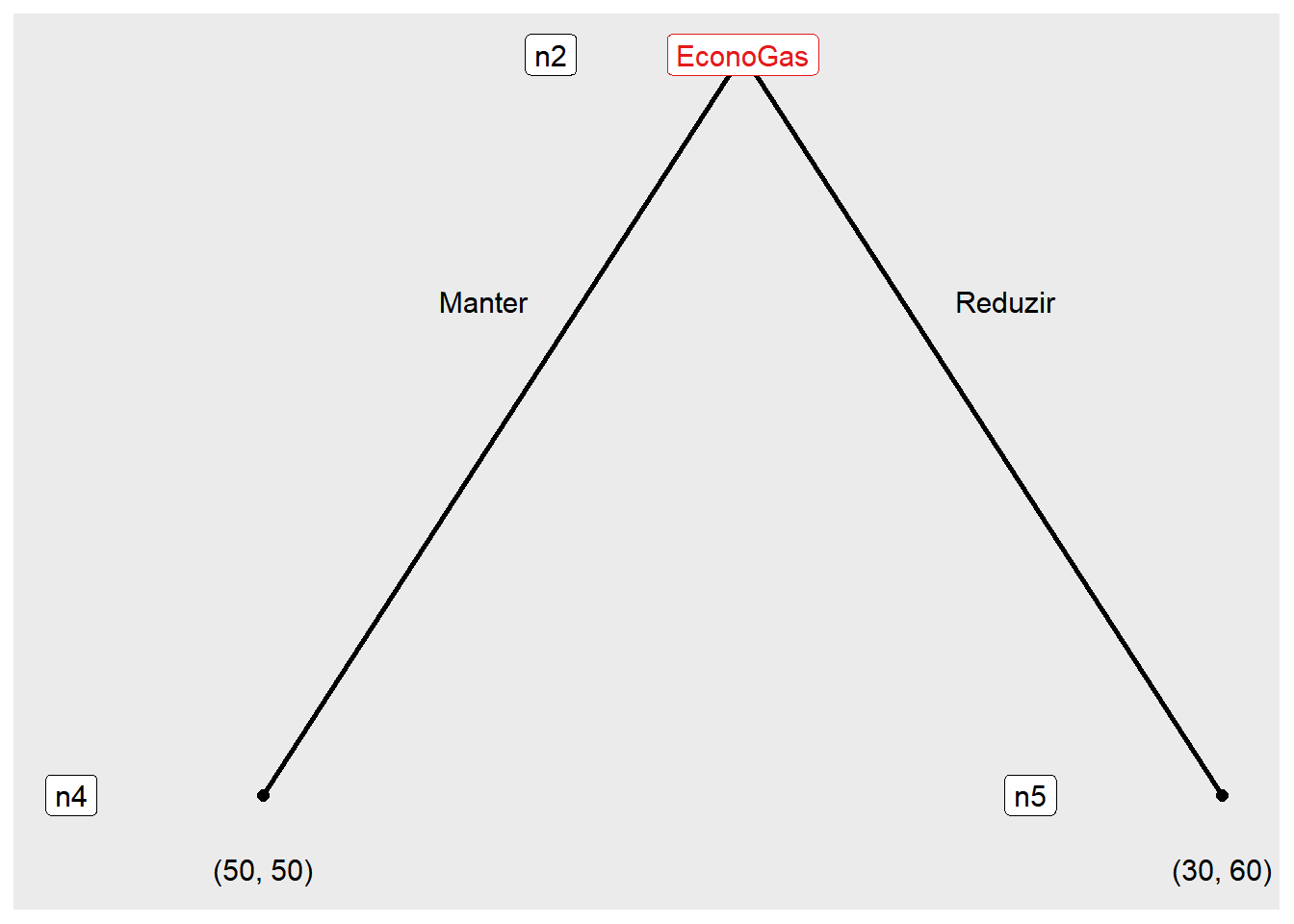
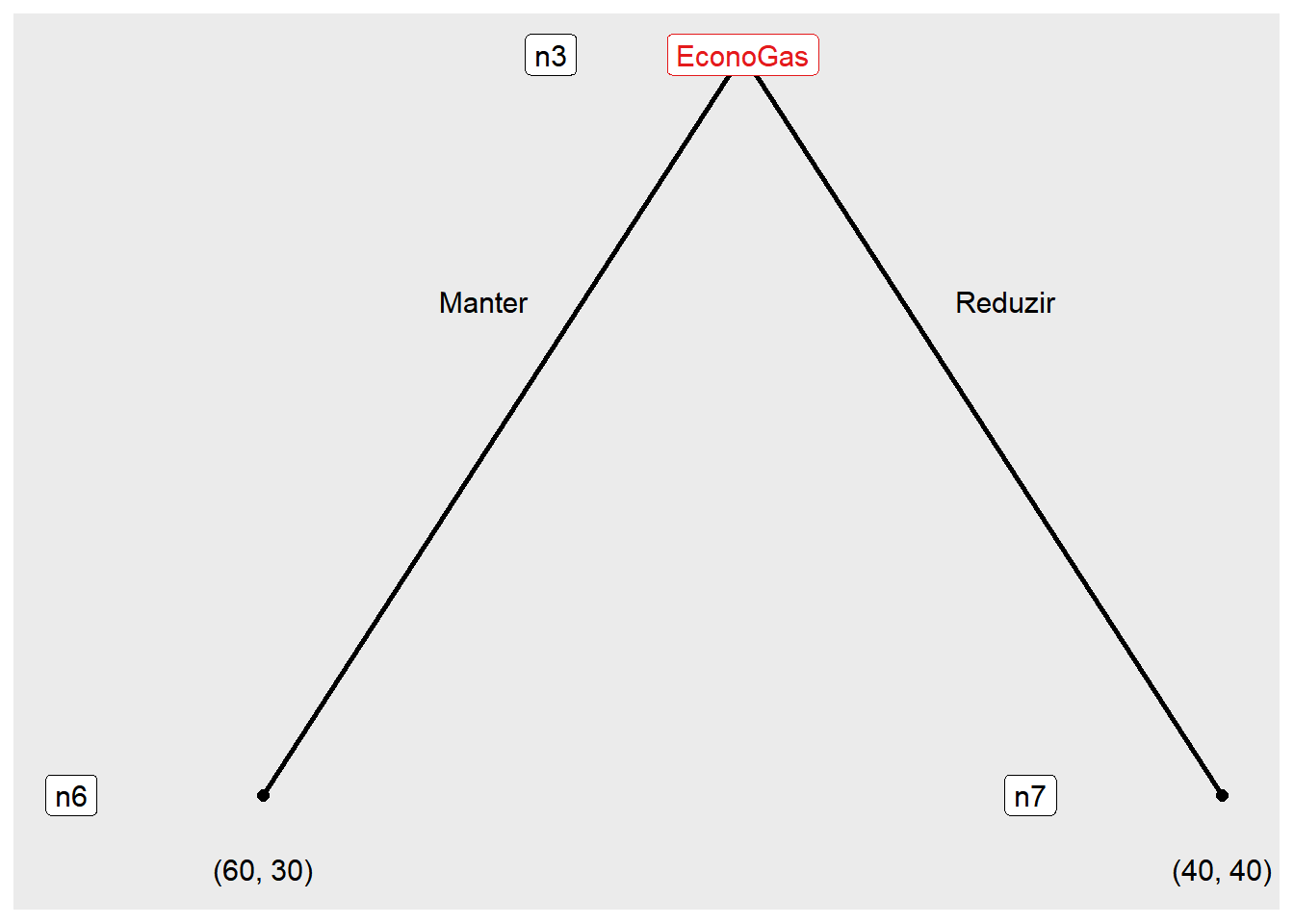
Ao utilizar o parâmetro quietly = FALSE, a mensagem de contagem de subjogos será exibida juntamente com os gráficos.
A função to_matrix é usada para transformar um jogo em forma extensiva, com dois jogadores, em um jogo em forma normal. Isso permite representar o jogo em uma matriz de ganhos, onde as estratégias ou perfis de ações são especificados.
jogo7mx <- to_matrix(jogo7)
Para visualizar o data frame que contém as matrizes dos jogadores 1 e 2, basta utilizar o objeto criado anteriormente, nomeado como jogo7mx, e acrescentar $df. Nesse data frame, as colunas payoff1 e s1 representam, respectivamente, os ganhos e as estratégias do posto OilFlex, enquanto as colunas payoff2 e s2 representam os ganhos e estratégias da EconoGas.
jogo7mx$df
row column s1 s2 payoff1 payoff2
1 1 1 (Manter) (Manter, Manter) 50 50
2 1 2 (Manter) (Manter, Reduzir) 50 50
3 1 3 (Manter) (Reduzir, Manter) 30 60
4 1 4 (Manter) (Reduzir, Reduzir) 30 60
5 2 1 (Reduzir) (Manter, Manter) 60 30
6 2 2 (Reduzir) (Manter, Reduzir) 40 40
7 2 3 (Reduzir) (Reduzir, Manter) 60 30
8 2 4 (Reduzir) (Reduzir, Reduzir) 40 40
Na visualização dos payoffs de cada jogador, é necessário utilizar a função matrix() em jogo7mx$mat$matrix1. Desse modo, é possível identificar as jogadas e os ganhos do jogador 1.
# Payoff do posto "OilFlex"
matrix(jogo7mx$mat$matrix1,
nrow = 2,
dimnames = list(c('M', 'R'),
c('MM', 'MR', 'RM', 'RR')))
MM MR RM RR
M 50 50 30 30
R 60 40 60 40
Ao utilizar o argumento dimnames para especificar os nomes das colunas e linhas de uma matriz. Dessa forma, é implementada por meio de uma lista, permitindo uma representação mais intuítiva das ações dos jogadores (Manter e Reduzir) e dos payoffs correspondentes ao jogador 1 e 2.
# Payoff do posto "EconoGas"
matrix(jogo7mx$mat$matrix2,
nrow = 2,
dimnames = list(c('M', 'R'),
c('MM', 'MR', 'RM', 'RR')))
MM MR RM RR
M 50 50 60 60
R 30 40 30 40
Quando utilizamos o argumento nrow = 2, estamos essencialmente informando que a matriz terá duas linhas, cada uma representando as ações “Reduzir” ('R') e “Manter” ('M'). Vale notar que, ao especificar o número de linhas, o ambiente R define automaticamente o número de colunas com base nessa especificação.
Eq. de Nash Perfeito em Subjogos
O Equilíbrio de Nash Perfeito em Subjogos (ENPS) é um conceito utilizado na teoria dos jogos para analisar estratégias em jogos sequenciais. Ele consiste em um conjunto de estratégias, uma para cada jogador, que representa um equilíbrio de Nash em cada subjogo do jogo original.
O solve_efg permite encontrar soluções para jogos em forma extensiva. Ele recebe como entrada um jogo em forma extensiva definido previamente e retorna uma lista de soluções encontradas, baseadas no conceito de solução escolhido pelo usuário.
Existem duas opções para o conceito de solução: "backward" (Indução Retroativa) e "spe" (Equilíbrio Perfeito em Subjogos), ambos obtêm o mesmo resultado.
solve_efg(jogo7, concept = "backward", quietly = FALSE)
backward induction: [(Reduzir), (Reduzir, Reduzir)]
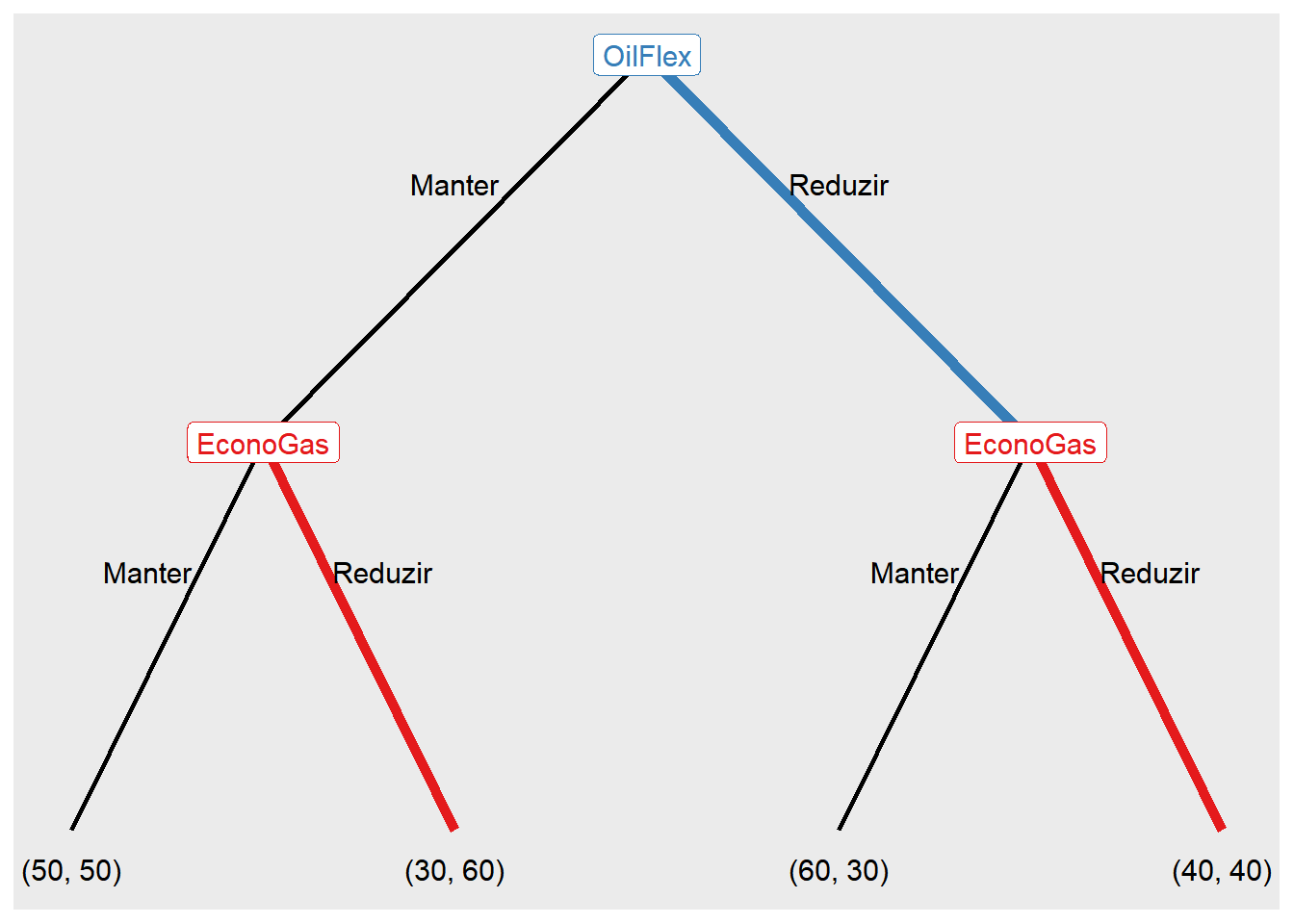
Ou pode-se chegar ao gráfico de melhores respostas pelo comando show_path().
show_path(jogo7)
Também é possível obter a tabela a partir da matriz usando a função solve_nfg() e determinar os equilíbrios de Nash e Equilíbrio de Nash Perfeito em Subjogos a partir das informações mencionadas no tópico anterior.
# Matriz do jogo 7
jogo7mxtab <- solve_nfg(jogo7mx)
Pure-strategy NE: [(Reduzir), (Reduzir, Reduzir)]
EconoGas |
|||||
|---|---|---|---|---|---|
| strategy | (Manter, Manter) | (Manter, Reduzir) | (Reduzir, Manter) | (Reduzir, Reduzir) | |
| OilFlex | (Manter) | 50, 50 | 50^, 50 | 30, 60^ | 30, 60^ |
| (Reduzir) | 60^, 30 | 40, 40^ | 60^, 30 | 40^, 40^ | |
Assim, o ENPS ocorre quando o posto EconoGas adota as estratégias de “Reduzir, Reduzir”, em resposta à redução de preços realizada pelo posto OilFlex.
O solve_seq aceita um jogo em forma sequencial como entrada e retorna os equilíbrios de Nash encontrados, se houver. Além disso, ele também pode exibir uma tabela com as jogadas e estratégias ótimas para cada jogador, facilitando a análise e compreensão dos resultados.
No exemplo anterior, utilizamos a função seq_form() para estruturar um jogo na forma sequencial, a partir de uma forma normal. Em seguida, aplicamos o solve_seq() para transformar o jogo da forma extensiva novamente para a forma normal.
solve_seq(
sq_jogo8,
show_table = TRUE,
mark_br = FALSE,
precision = 1L,
quietly = FALSE
)
SPE outcome: (Reduzir, Reduzir)
EconoGas |
|||
|---|---|---|---|
| strategy | Manter | Reduzir | |
| OilFlex | Manter | 50, 50 | 60, 30 |
| Reduzir | 30, 60 | 40, 40 | |
Já o argumento precision afeta a formatação dos valores exibidos na tabela de solução, determinando o número de casas decimais a serem apresentadas. Por exemplo, ao definir precision = 1L, os valores serão arredondados para uma casa decimal, já que o uso de 1L assegura que a precisão seja interpretada como um número inteiro.
Encontrar o ENPS envolve analisar cada subjogo, identificar os equilíbrios de Nash em cada um e verificar se esses equilíbrios são compatíveis entre si ao longo de todo o jogo. Caso exista um conjunto de estratégias que satisfaça essas condições, temos um Equilíbrio de Nash Perfeito em Subjogos.
Jogos Repetidos
Em jogos repetidos é possível definir os jogadores envolvidos e as ações disponíveis para cada um em cada rodada, de forma que os payoffs podem ser atribuídos a diferentes combinações de ações ao longo do tempo. Esse enfoque permite uma exploração mais profunda das complexas dinâmicas estratégicas que emergem quando os jogadores interagem repetidamente. À medida que eles se envolvem em múltiplas rodadas é ajustado suas estratégias com base nas escolhas anteriores dos adversários, construindo gradualmente um aprendizado estratégico.
Jogos Repetidos Finitos
Considerando um exemplo de jogo repetido finito entre dois países, "P1" e "P2", que estão em um cenário de possíveis conflitos e cooperação, representados pelas ações de “Guerra” ("G") e “Paz” ("P"). Nesse contexto, os jogadores estão envolvidos em quatro períodos de decisão. Eles estão avaliando se devem optar por “Guerra” ou “Paz” em cada período.
Comparando com a estrutura de Jogos Sequenciais, onde o argumento players continha rep() apenas no final e era definido por NA juntamente com o número de nós terminais. Em Jogos Repetidos, podemos utilizar a função rep() de forma mais detalhada.
Nesse caso, começamos com as jogadas de P2, pois as ações de P2 se repetirão sequencialmente após a ação do jogador inicial. Portanto, usamos "P2", 2 e assim por diante. Em sequência, teremos "P1", 4, o que significa que cada nó da jogada anterior de P2 se ramificará em dois nós, representando os 4 nós de P1. Na configuração rep(NA, 16), o valor NA indica que não há mais jogadas de nenhum jogador, apenas os nós terminais, que serão 16.
Nessa situação, especificamos duas estratégias para ambos os jogadores. Consequentemente, o número de repetições dos nós será sempre o dobro do anterior, como ilustrado abaixo.
jogo9 <- extensive_form(
players = list("P1", # n1
rep("P2", 2), # n2 e n3
rep("P1", 4), # n4 - n7
rep("P2", 8), # n8 - n15
rep(NA, 16)), # Nós terminais
actions = list(
c("G", "P"), c("G", "P"), c("G", "P"), # n1 - n3
c("G", "P"), c("G", "P"), c("G", "P"), # n4 - n6
c("G", "P"), c("G", "P"), c("G", "P"), # n7 - n9
c("G", "P"), c("G", "P"), c("G", "P"), # n10 - n12
c("G", "P"), c("G", "P"), c("G", "P") # n13 - n15
),
payoffs = list(
P1 = c(6, 5, 6, 4, 5, 3, 6, 2, 8, 4, 7, 6, 7, 3, 6, 4),
P2 = c(8, 5, 6, 4, 7, 5, 6, 8, 6, 2, 3, 3, 6, 3, 4, 7)
),
direction = "down",
show_node_id = FALSE
)
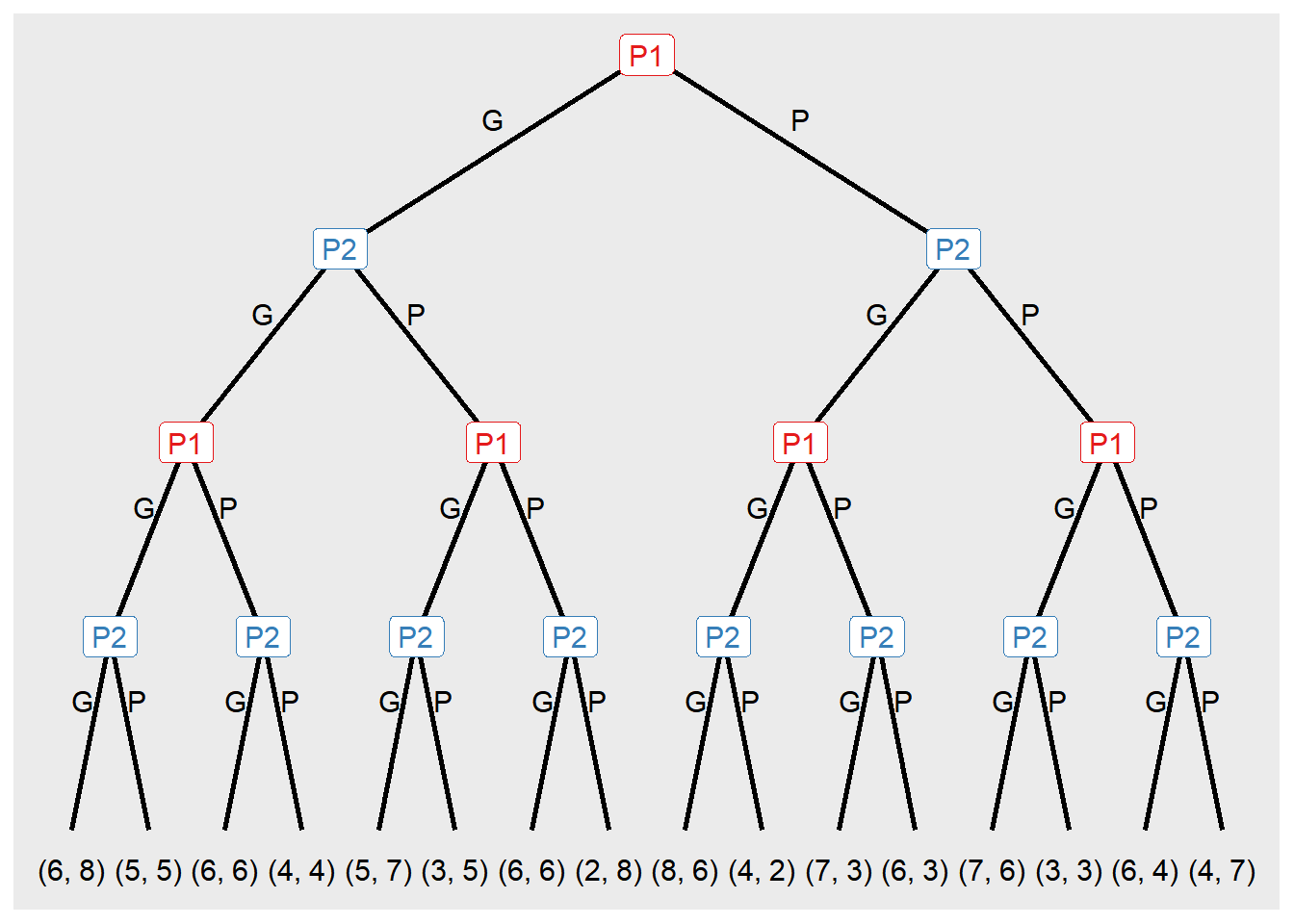
O exemplo acima possui uma estrutura de árvore com 15 nós, numerados de n1 a n15. Em cada nó, os jogadores têm a opção de escolher entre duas ações. Por exemplo, os três primeiros nós (n1 a n3) representam as escolhas de ação dos jogadores no primeiro período.
Ao resolver o jogo acima por indução retroativa é possível visualizar as estratégias escolhidas pelos dois jogadores.
s_jogo9 <- solve_efg(jogo9, concept = "backward", quietly = FALSE)
backward induction: [(P, G, G, G, G), (G, G, G, G, G, P, G, G, G, P)], [(P, G, G, G, G), (G, P, G, G, G, P, G, G, G, P)], [(P, P, G, G, G), (P, G, G, G, G, P, G, G, G, P)], [(P, P, G, G, G), (P, P, G, G, G, P, G, G, G, P)], [(P, G, G, G, G), (G, G, G, G, G, P, G, P, G, P)], [(P, G, G, G, G), (G, P, G, G, G, P, G, P, G, P)], [(P, P, G, G, G), (P, G, G, G, G, P, G, P, G, P)], [(P, P, G, G, G), (P, P, G, G, G, P, G, P, G, P)]
Em jogos repetidos, as árvores de decisão geralmente se tornam mais complexas, devido à repetição das jogadas pelos jogadores. Como observado anteriormente, foram identificadas oito soluções por meio da análise de indução retroativa.
s_jogo9$sols
[[1]]
[1] "[(P, G, G, G, G), (G, G, G, G, G, P, G, G, G, P)]"
[[2]]
[1] "[(P, G, G, G, G), (G, P, G, G, G, P, G, G, G, P)]"
[[3]]
[1] "[(P, P, G, G, G), (P, G, G, G, G, P, G, G, G, P)]"
[[4]]
[1] "[(P, P, G, G, G), (P, P, G, G, G, P, G, G, G, P)]"
[[5]]
[1] "[(P, G, G, G, G), (G, G, G, G, G, P, G, P, G, P)]"
[[6]]
[1] "[(P, G, G, G, G), (G, P, G, G, G, P, G, P, G, P)]"
[[7]]
[1] "[(P, P, G, G, G), (P, G, G, G, G, P, G, P, G, P)]"
[[8]]
[1] "[(P, P, G, G, G), (P, P, G, G, G, P, G, P, G, P)]"
Utilizando o nome do objeto criado, s_jogo9, em conjunto com o atributo $n_sols, é possível obter o número total de soluções, que neste contexto específico é representado como [1] 8. Em uma análise mais aprofundada de uma das soluções, podemos escolher a primeira solução por meio da combinação entre s_jogo9 e $trees[[1]], que corresponde à representação visual da solução $sols[[1]], ou seja, a primeira solução em formato de árvore.
s_jogo9$trees[[1]]
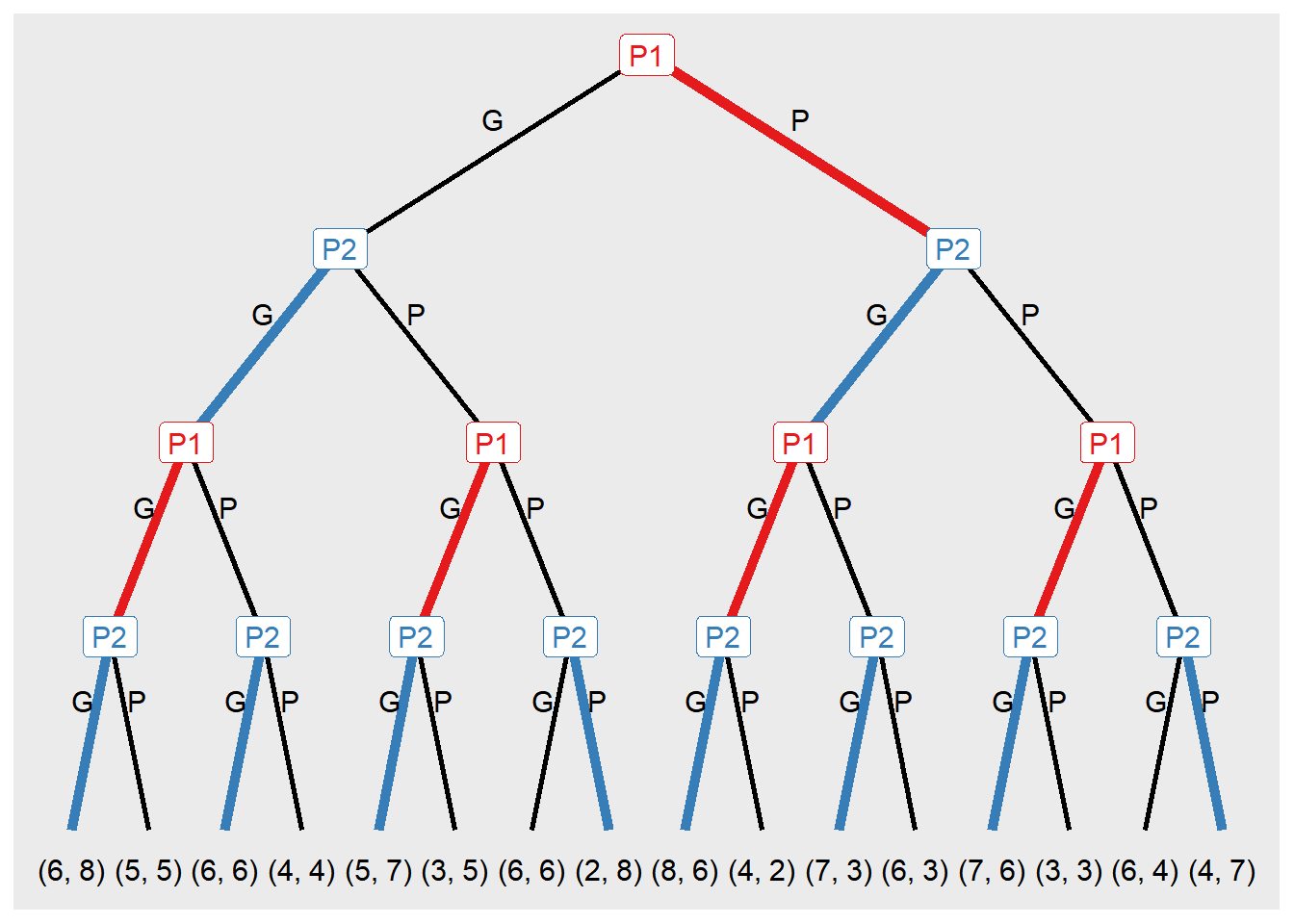
Para cada solução em formato de combinação ($sols) é possível se chegar a uma representação gráfica em árvore de decisão ($trees).
Os conjuntos de informações podem ser especificados no argumento info_sets, agrupando, dessa forma, os nós nos quais um jogador não consegue distinguir as ações tomadas por seu oponente. Por exemplo, os nós n2 e n3 formam um conjunto de informações para o jogador P1, indicando que ele não sabe qual ação o jogador P2 escolheu nos nós n2 e n3.
jogo9info <- extensive_form(
players = list("P1", # n1
rep("P2", 2), # n2 e n3
rep("P1", 4), # n4 - n7
rep("P2", 8), # n8 - n15
rep(NA, 16)), # Nós terminais
actions = list(
c("G", "P"), c("G", "P"), c("G", "P"), # n1 - n3
c("G", "P"), c("G", "P"), c("G", "P"), # n4 - n6
c("G", "P"), c("G", "P"), c("G", "P"), # n7 - n9
c("G", "P"), c("G", "P"), c("G", "P"), # n10 - n12
c("G", "P"), c("G", "P"), c("G", "P") # n13 - n15
),
payoffs = list(
P1 = c(6, 5, 6, 4, 5, 3, 6, 2, 8, 4, 7, 6, 7, 3, 6, 4),
P2 = c(8, 5, 6, 4, 7, 5, 6, 8, 6, 2, 3, 3, 6, 3, 4, 7)
),
direction = "down",
info_sets = list(c(2,3), c(8, 9), c(10, 11),
c(12, 13), c(14, 15)),
show_node_id = FALSE
)
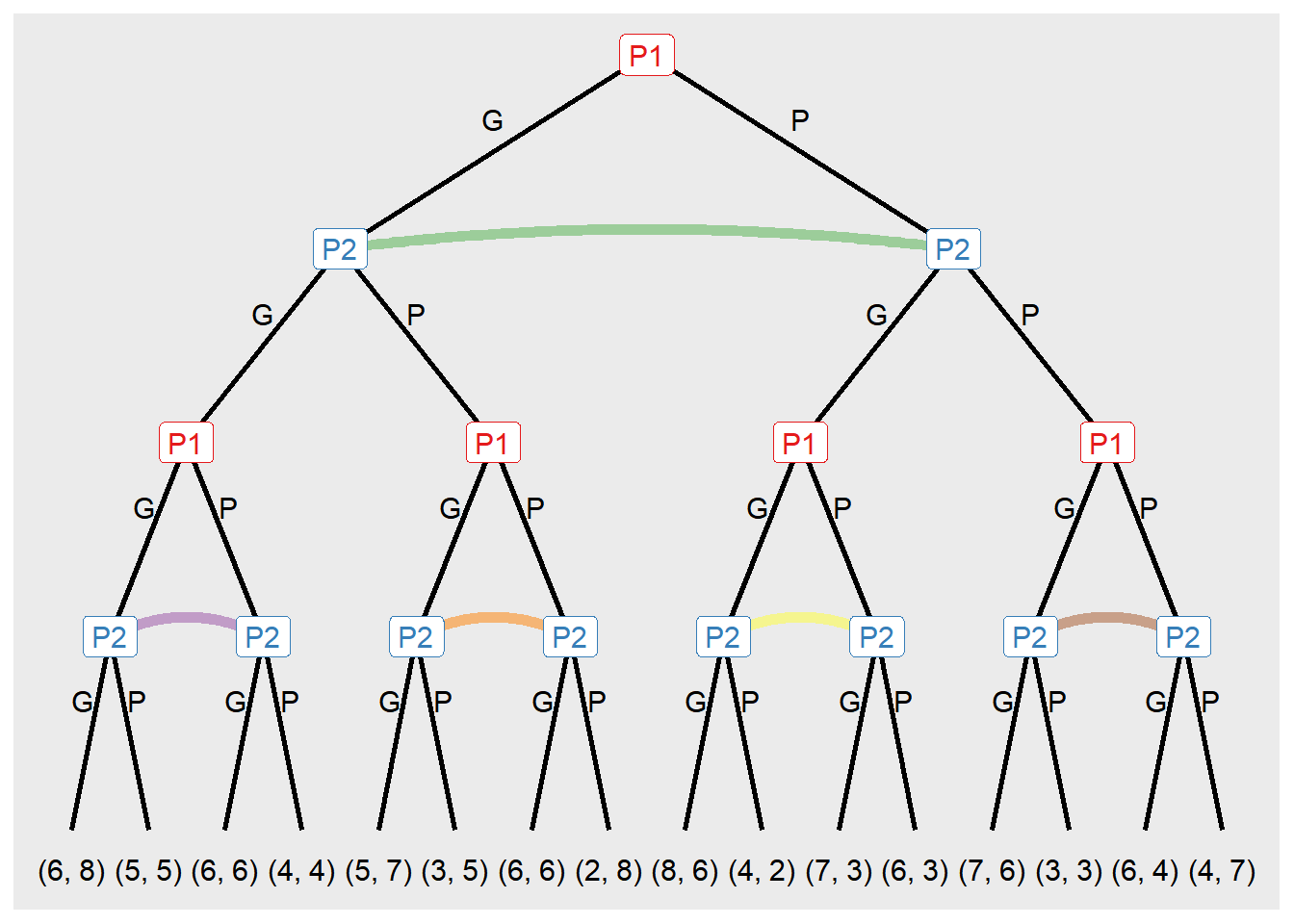
Devido à falta de conhecimento por parte do jogador P1 em relação às estratégias escolhidas pelo jogador P2, encontrar uma solução para esse jogo torna-se um desafio. Especialmente em cenários onde os jogadores estão alheios às estratégias dos demais participantes, como é o caso apresentado abaixo ao tentar aplicar o conceito de indução retroativa para elucidar as escolhas estratégicas de P1 e P2.
solve_efg(jogo9info, concept = "backward", quietly = FALSE)
Error in backward_induction(game, restriction = tree_overlay): This is not a perfect-information game.
Nesse caso, há um erro ao empregar a função backward_induction() ou solve_efg(), pois o jogo em questão não se encaixa na categoria de informação perfeita (Perfect-Information). Em restriction = tree_overlay ocorre a restrição de sobreposição na estrutura da árvore, especificamente pelo uso do parâmetro info_sets.
Em jogos de informação perfeita, os jogadores têm conhecimento completo sobre as ações e movimentos realizados por outros jogadores em cada ponto da árvore de decisão, como exemplo o jogo 7, 8 e 9. Se o jogo contém informações imperfeitas ou incertezas sobre as ações de outros jogadores, a indução reversa ou indução retroativa não pode ser aplicada diretamente, já que ela pressupõe informação perfeita.
Ao expandir o exemplo, agora com a introdução de um terceiro país "P3", novas dimensões estratégicas emergem. Nessa situação ele possui as opções de “Ajudar” ("A") e “Desestabilizar” ("D"). Se P3 escolher “Ajudar”, seu objetivo é promover uma abordagem cooperativa entre P1 e P2, encorajando tratados de paz e parcerias, podendo ser alcançado através de diplomacia, oferecendo incentivos econômicos ou compartilhando informações sensíveis.
Por outro lado, se P3 optar por “Desestabilizar”, suas ações terão como alvo a erosão da confiança entre P1 e P2, ou seja, ele poderia propagar rumores, incentivar disputas territoriais ou minar acordos já existentes. Ao fazer isso, será criado um ambiente de incerteza e rivalidade, aumentando assim as chances de conflito entre os outros dois países.
jogo10 <- extensive_form(
players = list("P1", # n1
rep("P2", 2), # n2 e n3
rep("P1", 4), # n4 - n7
rep("P2", 8), # n8 - n15
rep("P3", 16), # n16 - n31
rep(NA, 32)), # Nós terminais
actions = list(
c("G", "P"), c("G", "P"), c("G", "P"), # n1 - n3
c("G", "P"), c("G", "P"), c("G", "P"), # n4 - n6
c("G", "P"), c("G", "P"), c("G", "P"), # n7 - n9
c("G", "P"), c("G", "P"), c("G", "P"), # n10 - n12
c("G", "P"), c("G", "P"), c("G", "P"), # n13 - n15
# Ações do terceiro país (P3)
c("A", "D"), c("A", "D"), c("A", "D"), # n16 - n18
c("A", "D"), c("A", "D"), c("A", "D"), # n19 - n21
c("A", "D"), c("A", "D"), c("A", "D"), # n22 - n24
c("A", "D"), c("A", "D"), c("A", "D"), # n25 - n27
c("A", "D"), c("A", "D"), c("A", "D"), # n28 - n30
c("A", "D") # n31
),
payoffs = list(
P1 = c(6, 5, 6, 4, 5, 3, 6, 2,
8, 4, 7, 6, 7, 3, 6, 4,
8, 9, 1, 2, 3, 4, 5, 6,
7, 8, 9, 1, 2, 3, 4, 5),
P2 = c(8, 5, 6, 4, 7, 5, 6, 8,
6, 2, 3, 3, 6, 3, 4, 7,
8, 9, 1, 2, 3, 4, 5, 6,
7, 8, 9, 1, 2, 3, 4, 5),
P3 = sample(1:9, 32,
replace = TRUE)
),
direction = "right",
show_node_id = FALSE
)

Nesta situação, ocorre a expansão do exemplo ao adicionar mais 15 nodos, a fim de incluir o terceiro país no jogo. Além disso, a amostragem dos payoffs é estendida para 32 elementos. Uma abordagem alternativa é a definição dos payoffs de forma aleatória para P3, como realizado através da função sample(), a qual gera uma seleção aleatória de valores a partir de um vetor.
Ao empregar 1:9, 32 como argumento dessa função, é criado um vetor com valores variando de 1 a 9, ou seja, os possíveis ganhos do jogador P3 estão dentro desse intervalo. Esses valores são então repetidos 32 vezes, correspondendo ao número de elementos amostrados. A utilização de replace = TRUE permite que elementos sejam selecionados mais de uma vez na amostra, possibilitando a repetição de valores nos payoffs do país P3. Caso fosse definido replace = FALSE, cada valor apareceria apenas uma vez.
Em resumo, essa abordagem amplia a complexidade do exemplo ao adicionar um terceiro país e introduzir aleatoriedade nos payoffs desse jogador por meio da função sample().
s_jogo10 <- solve_efg(jogo9, concept = "backward", quietly = FALSE)
backward induction: [(P, G , G , G , G ), (G, G, G , G , G , P, G , G , G , P)], [(P, G , G , G , G ), (G, P, G , G , G , P, G , G , G , P)], [(P, P, G , G , G ), (P, G, G , G , G , P, G , G , G , P)], [(P, P, G , G , G ), (P, P, G , G , G , P, G , G , G , P)], [(P, G , G , G , G ), (G, G, G , G , G , P, G , P, G , P)], [(P, G , G , G , G ), (G, P, G , G , G , P, G , P, G , P)], [(P, P, G , G , G ), (P, G, G , G , G , P, G , P, G , P)], [(P, P, G , G , G ), (P, P, G , G , G , P, G , P, G , P)]

A presença de P3 adiciona uma nova camada de complexidade. Sua escolha de “Ajudar” em vez de “Desestabilizar” parece ter desempenhado um papel crucial em incentivar a paz entre P1 e P2 nas primeiras rodadas. No entanto, à medida que P1 opta por “Guerra” e P2 responde da mesma forma, o equilíbrio entre os três países se torna mais delicado.
Em síntese, a introdução de P3 com suas estratégias de “Ajudar” e “Desestabilizar” transformou a dinâmica geopolítica. As decisões agora são influenciadas pelas ações de três jogadores, levando a resultados variados e demonstrando como diferentes abordagens podem levar a cenários diversos de cooperação e conflito
Quando se trata de um jogo com três jogadores, como no caso do jogo 9, a função to_matrix() não pode ser empregada, conforme demonstrado na tentativa a seguir ao utilizá-la.
to_matrix(jogo10)
Error in to_matrix(jogo10): This function only works with a two-person game.
Esse erro ocorre pois a função to_matrix() do pacote Rgamer é projetada para trabalhar com jogos de dois jogadores. A mensagem de erro que está sendo mostrada, “This function only works with a two-person game”, significa que essa função não é capaz de lidar com jogos envolvendo três jogadores ou mais, pois limita-se a jogos de dois jogadores porque ela transforma a estrutura de um jogo em uma matriz, que é mais adequada para jogos de dois jogadores.
Quando há três jogadores, como no exemplo apresentado, a representação em forma extensiva da árvore de decisão se torna mais clara e menos complexa do que a representação em forma normal por matriz, porém a complexidade aumenta ao considerar as possíveis soluções de indução retroativa, em que cada jogador analisa as escolhas dos outros para determinar suas próprias ações.
Com três ou mais jogadores, a quantidade de combinações possíveis de soluções de indução retroativa cresce exponencialmente. Desse modo, surge mais cenários estratégicos a considerar, tornando impraticável a representação por matriz.
Referências
YANAI, Yusei; KAMIJO, Yoshio. Game Theory With R. Shin-Ogawacho, Shinjuku-ku, Tóquio, JP: Asakura Publishing Co,. Ltd., 2023. 244 p. ISBN 978-4-254-27024-2 C3050.
